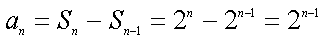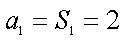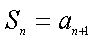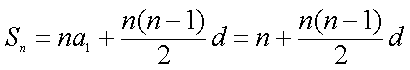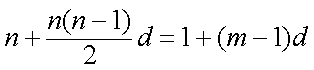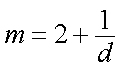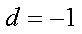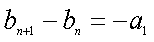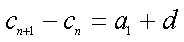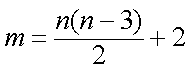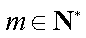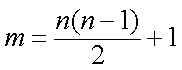- 等差数列的性质及应用
- 共237题
设数列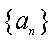
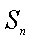
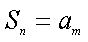
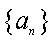
(1)若数列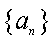
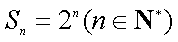
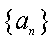
(2)设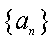
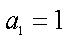
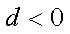
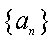
(3)证明:对任意的等差数列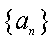
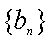
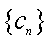
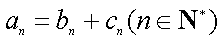
正确答案
见解析。
解析
(1)当
当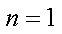
∴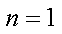
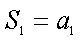

∴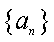
(2)
对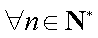
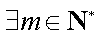
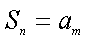
取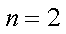
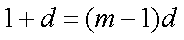
∵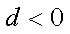
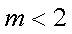
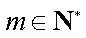
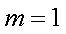
(3)设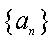
令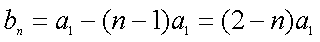
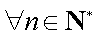
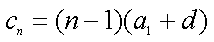
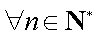
则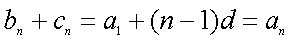
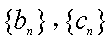
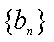
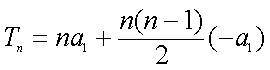
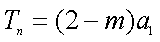
当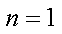
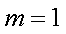
当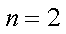
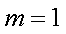
当
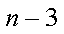
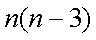
因此对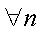
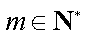
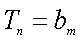
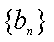
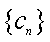
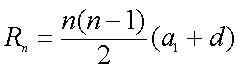
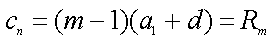
∵对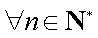
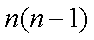
即对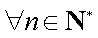
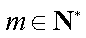
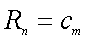
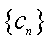
因此命题得证.
知识点
在等差数列


(1)求数列
(2)设数列





正确答案
见解析
解析
(1)设等差数列

依题意 

所以 

所以数列

(2)由数列


得 

所以 
所以

从而当

当

知识点
已知集合









(1)求数列
(2)若数列

求
正确答案
见解析。
解析
(1)由题设知: 集合





由此可得,对任意的



设等差数列


因为

由于


所以

所以数列


(2)
于是有

知识点
已知



(1)求数列
(2)记数列





正确答案
见解析
解析
(1)由题,设


由

即




所以数列

(2)由(1)得,

则

由

知识点
如图,在底面是矩形的四棱锥P—ABCD中,PA⊥面ABCD,E是PD的中点.
(1)求证:平面PDC⊥平面PDA;
(2)求几何体P—ABCD被平面ACE分得的两部分的体积比
正确答案
见解析。
解析
(1)∵

∴
∵四边形ABCD是矩形.
∴

又∵CD

(2)由已知

知识点
扫码查看完整答案与解析