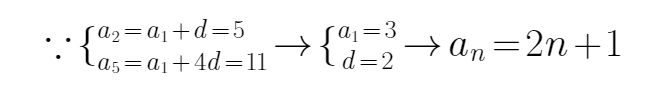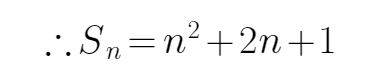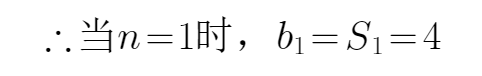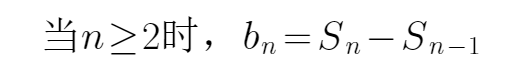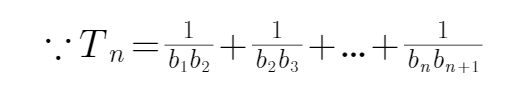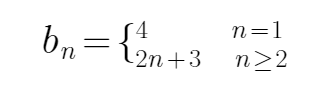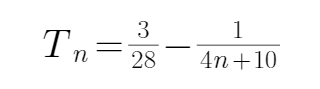- 数列的概念与简单表示法
- 共1089题
已知数列




17.求数列
18.设




正确答案
(1)
解析
(Ⅰ)当


当


显然当
∴
考查方向
解题思路
先令



易错点
1.不会转化题中的条件

正确答案
(2)
解析
(Ⅱ)∵
∴
考查方向
解题思路
由第(1)问的结果可以得到
易错点
不明白
已知数列








24.比较


25.证明:

正确答案
解析
由

两式相减得:

又

∴

即:
考查方向
解题思路
先由通项及数列的前n项和的关系,求出通项,再求和,进而得出数列
易错点
在利用数列的前n项和与通项的关系时,易忽略对首项的验证
正确答案
略
解析
解:由(Ⅰ)知:

因此当

则
----------------------------------11分
又∵当

当且仅当
∴
∴

考查方向
解题思路
逐级对数列{






易错点
在构造数列放缩时,放缩不合理,导致出错
已知数列



17.求数列
18.若



正确答案
an=22n-1;
解析
试题分析:本题属于等差数列通项求法与求和的应用问题,题目的难度适中。(1)求解时一定要灵活应用




(Ⅰ)由
当
当


所以数列


考查方向
解题思路
本题考查了等差数列的通项公式和求和公式的应用及性质,解题步骤如下:
由数列前



对于

易错点
由数列前


正确答案
证明略。
解析
试题分析:本题属于等差数列通项求法与求和的应用问题,题目的难度适中。(1)求解时一定要灵活应用




由(Ⅰ)可得
当
当

综上,
考查方向
解题思路
本题考查了等差数列的通项公式和求和公式的应用及性质,解题步骤如下:
由数列前



对于

易错点
由数列前


17. 在等差数列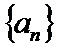

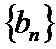
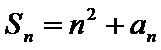
(Ⅰ)求数列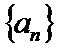
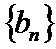
(Ⅱ)求数列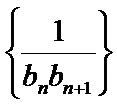
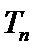
正确答案
见解析
解析
解:
经验证首项不成立
(2)当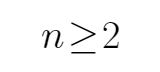
验证: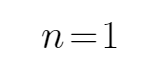
考查方向
主要考察了等差数列的性质及应用,考察了sn与an之间的关系,考察了裂项相消法求和
解题思路
第一步:通过等差数列的性质求出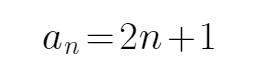
第二步:根据bn的通项公式可知,当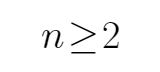
第三步:使用裂项相消的方法得到
易错点
该题在求bn过程中忽略了首项不成立,第二问求Tn的过程中忽略从第二项起,且使用分组的形式书写答案
教师点评
该题主要考察了讨论首项的数列,解题过程中要注意利用前n项和求通项一定要验证首项。
其次,分段数列在求前n项和的时候不需要把n=1独立出来
知识点
已知数列






22.分别求数列

23.若



正确答案
(1)

解析
(Ⅰ)


又因为

设等比数列

由已知

解得


所以,
考查方向
解题思路
先利用已知数列的前n项和求通项公式求出

易错点
1.不会利用数列的前n项和求通项公式;2.对于数列
正确答案
(2)
解析
(Ⅱ)
设数列





当
当


则

1-2得
所以
所以,
考查方向
解题思路
先由第(1)问得到
易错点
1.不会利用数列的前n项和求通项公式;2.对于数列
15.数列





正确答案
考查方向
解题思路
1. 当
易错点
当

知识点
设数列




17.求数列
18.求数列


正确答案
详见解析
解析
(1)由题意得:
当

①-②得


由①式中令

∴数列
∴
考查方向
等差数列的性质 等差数列的通项公式
解题思路
利用Sn和an之间的关系,化简变形求得答案
易错点
相关公式掌握不牢,记忆混淆
正确答案
详见解析
解析
(2)由
∴
考查方向
数列求和
解题思路
先表示出Tn的数列表示形式,然后求得2Tn 和-Tn,两式相加,得到数列Tn的表达式
教师点评
观察 猜想 证明,“试试看”是解决这类问题的关键
某企业在一次物业管理项目的招标活动中,根据《中华人民共和国招标投标法》的要求安排了以下招标程序:①成立招标组织;②组织投标人踏勘现场,并对招标文件答疑;③签收投标文件;④编制招标文件和标底;⑤确定投标人编制投标文件所需要的合理时间;⑥发布招标公告或发出投标邀请书;⑦发售招标文件;⑧对潜在投标人进行资质审查,并将审查结果通知各潜在投标人。下列排列顺序正确的是( )。
A.①②③④⑤⑥⑦⑧
B.①④⑥⑧⑦②⑤③
C.①④⑧③②⑥⑤⑦
D.①⑧⑥④⑤②⑦③
正确答案
B
解析
暂无解析
19. 设数列






(1)求证:数列

(2)令








正确答案
见解析
解析
解:(1)当


代入

而
∴数列
∴


又
(2)当



∴
故
当

若
则等式


若


∵



∴当且仅当


综上可知,当


当


考查方向
解题思路
利用

易错点
忽略n的范围的讨论。
知识点
已知集合


正确答案
解析
略
考查方向
集合
解题思路
集合
知识点
扫码查看完整答案与解析