- 圆的参数方程
- 共24题
7.若直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知直线l的参数方程为

(1)求直线l和圆C的普通方程;
(2)若直线l与圆C有公共点,求实数a的取值范围。
正确答案
(1)直线l的参数方程为
圆C的参数方程为
(2)圆心C(0,0),半径r=4。
由点到直线的距离公式可得圆心C(0,0)到直线L的距离d=
∵直线L与圆C有公共点,∴d≤4,即


解析
选作题;坐标系和参数方程。
(1)消去参数,把直线与圆的参数方程化为普通方程;
(2)求出圆心到直线的距离d,再根据直线l与圆C有公共点⇔d≤r即可求出。
知识点
若


正确答案
45°或
解析
略
知识点
已知






正确答案
解析
略
知识点
如图,以过原点的直线的倾斜角θ为参数,则圆x2+y2-x=0的参数方程为__________。
正确答案

解析
解析:由三角函数定义知



知识点
若以






正确答案
解析
曲线


圆心到直线距离


知识点
在极坐标系中,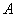
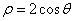
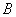
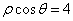
正确答案
2
解析
略
知识点
选修44:坐标系与参数方程
正确答案
解析
知识点
扫码查看完整答案与解析













