- 不等式的性质
- 共307题
已知关于

(1)当
(2)若此不等式的解集为

正确答案
(1)
解析
(1)当

由绝对值的几何意义知,不等式的意义可解释为数轴上的点
于2.∴


注 也可用零点分段法求解。
(2)∵
∴原不等式的解集为R等价于



∴
知识点
不等式选讲已知函数
(1)当

(2)若关于



正确答案
(1)
解析
(1) 


则不等式等价于


解之得




(2) 

由题意,不等式

则

而


知识点
在平面直角坐标系中,







正确答案
解析
略
知识点
对于任意的x∈ R,不等式

正确答案
解析
略
知识点
已知变量x,y满足
正确答案
解析
略
知识点
不等式组
正确答案
解析
略
知识点
设变量x,y满足约束条件
正确答案
解析
略
知识点
设函数

(1) 求不等式
(2) 如果关于



正确答案
(1)[-2,14](2)
解析
(1) 

当



当



当 



综上可得,不等式的解集为
(2)设







若

知识点
不等式组


正确答案
解析
略
知识点
已知函数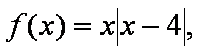
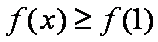
正确答案
解析
略
知识点
扫码查看完整答案与解析