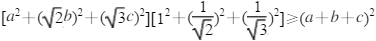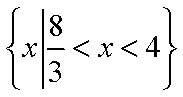- 不等式的性质
- 共307题
1
题型:
单选题
|
已知实数x,y满足条件
正确答案
D
解析
要求



知识点
不等式的性质
1
题型:简答题
|
已知a,b,cR,a2+2b2+3c2=6,求a+b+c的最大值。
正确答案
见解析。
解析
由柯西不等式,得
因为a2+2b2+3c2=6,所以(a+b+c)2≤11,
所以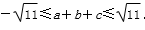
所以a+b+c的最大值为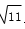
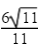
知识点
不等式的性质
1
题型:简答题
|
已知函数
(1)求函数
(2)若不等式

正确答案
见解析。
解析
(1)
令
令
故函数

(2)
令
又
令
当x在


由表知,当

所以,
知识点
不等式的性质
1
题型:简答题
|
已知函数
(1)当m=2时,求曲线
(2)若

正确答案
见解析。
解析
(1)m=2时,
切点坐标为(1,0),∴切线方程为
(2)m=1时,令
∴
又


∴方程
(或说明
(3)由题意知,

则当

令


则




则m的取值范围是
知识点
不等式的性质
1
题型:填空题
|
已知不等式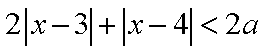
(1)若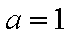
(2)若不等式的解集不是空集,则实数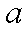
正确答案
(1)
(2)
解析
(1)当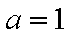
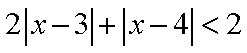
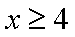
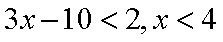

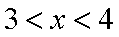
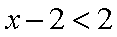
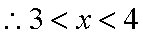
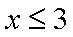
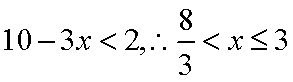
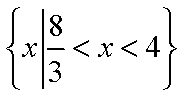
(2)设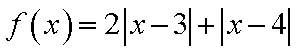
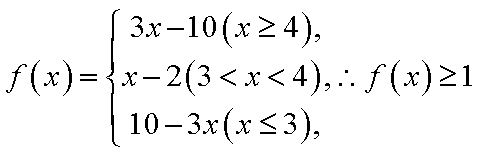
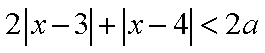
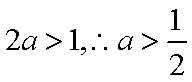
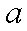
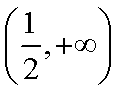
知识点
不等式的性质
下一知识点 : 不等式的应用
扫码查看完整答案与解析