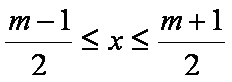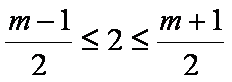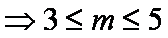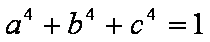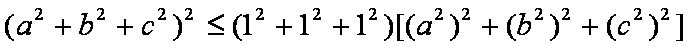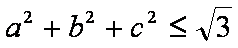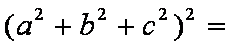- 不等式的性质
- 共307题
已知关于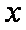
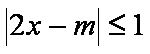
(1) 求整数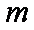
(2)已知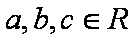
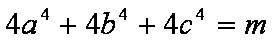
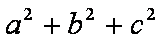
正确答案
(1)4
(2)当且仅当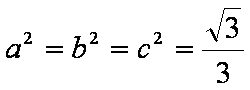
解析
(1)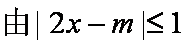
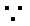
∴
又不等式仅有一个整数解2, ∴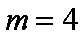
(2)显然
由柯西不等式可知;
所以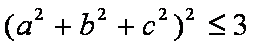
当且仅当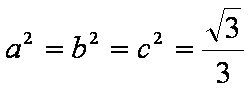
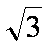
解法二:可平方,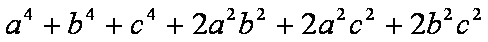
知识点
若关于


正确答案
解析
略
知识点
设关于x,y的不等式组
正确答案
解析
略
知识点
已知


正确答案
解析
略
知识点
设函数
(1)求证:当
(2)关于x的不等式
正确答案
见解析。
解析
(1) 证明:由
得函数


(2) 由绝对值的性质得
所以





知识点
已知6枝玫瑰与3枝康乃馨的价格之和大于24元,而4枝玫瑰与4枝康乃馨的价格之和小于20元,那么2枝玫瑰和3枝康乃馨的价格的比较结果是( )
正确答案
解析
略
知识点
已知函数

(1)若函数


(2)若函数

正确答案
见解析。
解析
(1)当


∵

∴
解得:

(2)
即存在

使得

则有

化简得:


设
∵
∴当


即


∴



即

∴


∴

知识点
若






正确答案
解析
由于







知识点
设函数



①
②
③
④


正确答案
解析
略
知识点
已知关于

(1)当
(2)若此不等式的解集为

正确答案
(1)
解析
(1)当

由绝对值的几何意义知,不等式的意义可解释为数轴上的点
于2.∴


注:也可用零点分段法求解。
(2)∵
∴原不等式的解集为R等价于



∴
知识点
扫码查看完整答案与解析