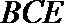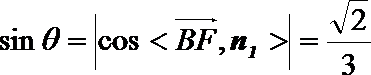- 用空间向量求直线与平面的夹角
- 共2题
1
题型:简答题
|
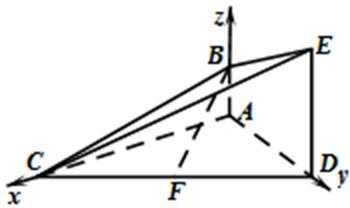
19.已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等腰直角三角形,AC⊥AD,且AD=DE=2AB,F为CD中点。
(Ⅰ)求证:平面BCE⊥平面CDE;
(Ⅱ)求直线BF和平面BCE所成角的正弦值。
正确答案
以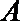
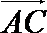
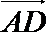
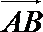
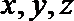
设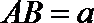
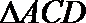
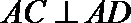
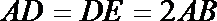
所以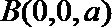
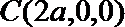
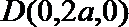
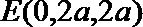
所以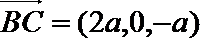
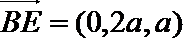
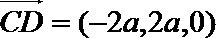
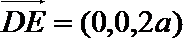
(Ⅰ)设平面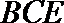
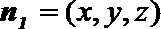
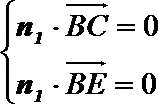
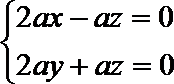
令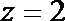
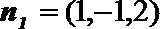
设平面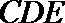
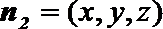
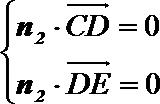
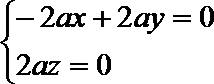
令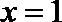
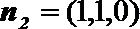
所以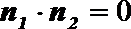
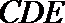
(Ⅱ)因为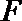
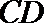
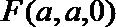
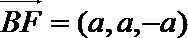
则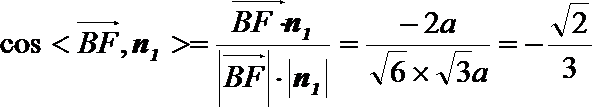
设直线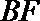
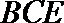
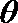
所以直线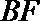
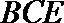
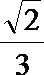
解析
解析已在路上飞奔,马上就到!
知识点
平面与平面垂直的判定与性质用空间向量求直线与平面的夹角
1
题型:
单选题
|
10.直三棱柱


△



正确答案
C
解析
由题意设底面正△ABC的边长为a,过P作PO⊥平面ABC,垂足为O,则点O为底面△ABC的中心,故∠PAO即为PA与平面ABC所成角。
又直三棱柱的体积为
所以只棱柱体积为
所以PA与平面ABC所称的角为
考查方向
直线与平面所成的角;棱柱、棱锥、棱台的体积
解题思路
由题意设底面正△ABC的边长为a,过P作PO⊥平面ABC,垂足为O,则点O为底面△ABC的中心,故∠PAO即为PA与平面ABC所成角,由此能求出PA与平面ABC所成的角.
易错点
空间感不强,计算化简能力弱
知识点
用空间向量求直线与平面的夹角
下一知识点 : 用空间向量求平面间的夹角
扫码查看完整答案与解析