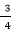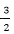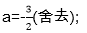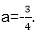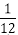- 奇偶函数图象的对称性
- 共31题
5.函数
正确答案

解析



考查方向
解题思路
列出满足要求的不等式,利用不等式求解
易错点
列出所有满足要求的不等式
知识点
11.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知定义域为R的函数f(x)的图象关于x=1对称,且当x>1时,f'(x)<0恒成立,又f(3)=0,则(x-2)f(x+3)<0的解集为( )
正确答案
解析
根据条件可构造函数f(x)=-(x-1)2+4,
则不等式(x-2)f(x+3)<0可化为(x-2)(-x2-4x)<0,
即(x-2)(x2+4x)>0,
解得-4<x<0或x>2,
所以原不等式的解集为(-4,0)∪(2,+∞).
知识点
3.已知实数a≠0,函数
正确答案
解析
当a>0时,2-2a+a=-1-a-2a,
解得
当a<0时,-1+a-2a=2+2a+a,
解得
知识点
3.已知实数a≠0,函数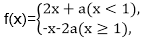
正确答案
解析
当a>0时,2-2a+a=-1-a-2a,
解得
当a<0时,-1+a-2a=2+2a+a,
解得
知识点
6.若函数f(x)=
正确答案
解析
因为f(x)=



知识点
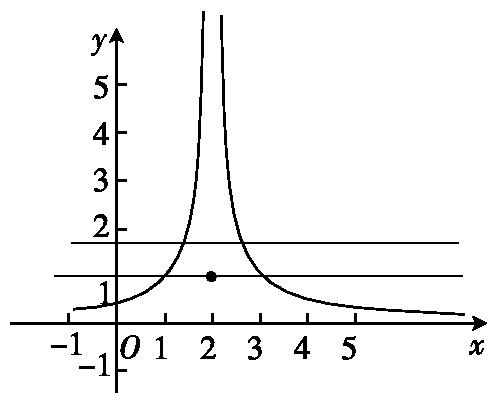
5.定义在R上的函数f(x)=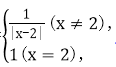
正确答案
解析
方程f2(x)-mf(x)+m-1=0的解是f(x)=1或f(x)=m-1>1.在坐标系中画出函数f(x)的图象,以及直线y=1,y=m-1(如图所示).由图象可知函数f(x)的图象与直线y=1,y=m-1有五个不同的公共点,即方程f2(x)-mf(x)+m-1=0有五个不同的实根.设x1<x2<x3<x4<x5,则x1+x5=x2+x4=4,x3=2,所以f(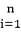


知识点
15. 有四个命题:
①函数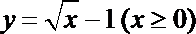
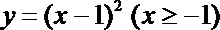
②函数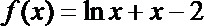
③函数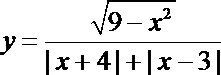
④若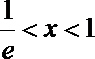
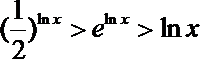
其中真命题的序号是________.
正确答案
③④
解析
解析已在路上飞奔,马上就到!
知识点
15.已知






正确答案
5
解析
根据函数大致图形,由已知条件可知,函数在没两个区间长度的区间范围内就有一个零点,所以在[0,10]上有5个零点,所以填5
考查方向
解题思路
先根据题意作出大致图象,利用图象结合函数性质求得。
易错点
函数零点考虑情况不完全
知识点
12.函数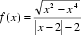
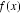
①函数的定义域和值域均为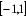
②函数的图像关于原点成中心对称;
③函数在定义域上单调递增;
④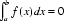
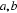
⑤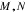
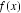
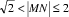
则关于函数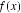
正确答案
解析
根据已知解析式可知,
函数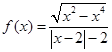
因为-1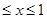
那么原式化简为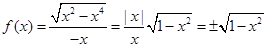
然后分析函数的定义域和值域均为
函数是奇函数,可知关于原点成中心对称,
同时在定义域内递增,并且命题4,利用对称性可知定积分值为零,
命题5中,不成立,故正确的序号为②④。
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
本题主要考查函数的性质
解题思路
1、化简函数解析式;
2、依次判断每个命题,即可得到结果。
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
本题易在判断化简时发生错误。
知识点
扫码查看完整答案与解析