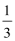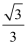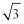- 量积判断两个平面向量的垂直关系
- 共78题
在平面直角坐标系







(1)求


(2)记四边形


(3)对于(2)中的




正确答案
见解析
解析
解析:(1)由已知条件得,



设

所以

即



(证明

(2)由(1)得

设




所以
设直线




(3)由(2)

于是,

数列







知识点
在平面直角坐标系xOy中,设动点P,Q都在曲线C:
点对应的参数分别为θ=α与θ=2α(0<α<2π),设PQ的中点M与定点A(1,0)间的距离为d,
求d的取值范围。
正确答案
见解析。
解析
由题设可知P ( 1 + 2cosα,2sinα ),Q ( 1 + 2cos2α,sin2α ),
于是PQ的中点M
从而
因为0<α<2π,所以-1≤cosα<1,
于是0≤d 2<4,故d的取值范围是
知识点
在极坐标系中,点

正确答案
解析
略
知识点
在平面直角坐标系xOy中,“直线


“ ”。
正确答案
解析
易得


知识点
在





(1)求角
(2)当

正确答案
见解析
解析
(1)由

由正弦定理得



(2)

由

即


知识点
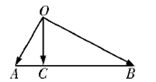
已ΔABC的内角A,B,C对的边分别为 a,b,c 



(1)求角A的大小;
(2)若a = 1,求b +c的取值范围.
正确答案
(1)
解析
(1)由


再由正弦定理得:
又
所以
又
(2)由正弦定理得


故b+c的取值范围为(1,2] . ……12分
知识点
16.已知向量


(1)求

(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.在







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知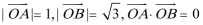

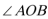
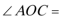

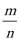
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析