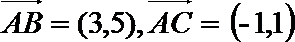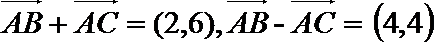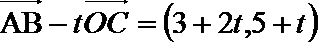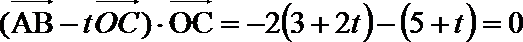量积判断两个平面向量的垂直关系
共78题

· 量积判断两个平面向量的垂直关系

量积判断两个平面向量的垂直关系
共78题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

10．已知是坐标原点，是平面上的两点，且，。若△是直角三角形，则_________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平面向量数量积的运算量积判断两个平面向量的垂直关系

题型：简答题

简答题 · 10 分

17．在平面直角坐标系中,.

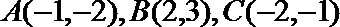
（1）求以线段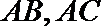为邻边的平行四边形的两条对角线的长;

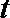
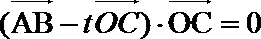
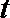
（2）设实数满足,求的值。

正确答案

（1）因为

则

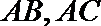
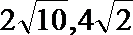
以线段为邻边的平行四边形的两条对角线的长分别为.

（2）因为

所以

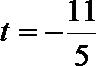
解析

解析已在路上飞奔，马上就到！

知识点

向量的模向量的加法及其几何意义向量的减法及其几何意义平面向量数量积的运算量积判断两个平面向量的垂直关系

题型：简答题

简答题 · 13 分

20.已知以原点O为中心的椭圆，它的短轴长为，右焦点(c>0)，它的长轴长为2a(a>c>0)，直线与x轴相交于点A，，过点A的直线与椭圆相交于P.Q两点。

（Ⅰ）求椭圆的方程和离心率；

（Ⅱ）若，求直线PQ的方程；

（Ⅲ）设，过点P且平行于直线的直线与椭圆相交于另一点M，证明：。

正确答案

(Ⅰ)解：由题意，可知椭圆的方程为.

由已知得

解得，c=2，

所以椭圆的方程为，离心率.

(Ⅱ)解：由（1）可得A(3，0)．设直线PQ的方程为y=k(x－3).

联立方程组，得(3k2+1)x2－18k2x+27k2－6=0，

依题意△=12(2－3k2)>0，得.

设P(x1，y1)，Q(x2，y2)，则

， ①

． ②

由直线PQ的方程得为y1=k(x1－3)，y2=k(x2－3)，于是，

y1y2=k2(x1－3) (x2－3)= k2[x1x2－3(x1+ x2)+9]. ③

∵，∴x1x2+y1y2=0． ④

由①②③④得5k2=1，从而．

所以直线PQ的方程为或．

(理科做)

(Ⅲ)证明：∵P(x1，y1)，Q(x2，y2)， A(3，0)，

∴，．由已知得方程组

，注意λ>1，解得，

因为F(2，0)， M(x1，－y1)，故

而，所以.

解析

解析已在路上飞奔，马上就到！

知识点

平面向量数量积的运算量积判断两个平面向量的垂直关系椭圆的定义及标准方程椭圆的几何性质直线、圆及圆锥曲线的交汇问题

题型：填空题

填空题 · 4 分

9．已知等比数列的公比不为1，其前项和为，若向量，，满足，则___________．

正确答案

121

解析

解析已在路上飞奔，马上就到！

知识点

平面向量数量积的运算量积判断两个平面向量的垂直关系等比数列的基本运算等比数列的性质及应用数列与向量的综合

题型：单选题

单选题 · 5 分

7．在矩形ABCD中，，，设，，当时，求得的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平面向量数量积的运算量积判断两个平面向量的垂直关系

题型：单选题

单选题 · 5 分

8．称为两个向量．间的“距离”，若向量．满足:

①;

②;

③对任意的,恒有

则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

向量的模单位向量相等向量与相反向量量积判断两个平面向量的垂直关系

题型：单选题

单选题 · 5 分

8．已知向量a=（2，1），b=（－1，k），a·（2a－b）=0，则k=（）

A－12

B－6

D12

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平面向量的坐标运算平面向量数量积的运算量积判断两个平面向量的垂直关系

题型：填空题

填空题 · 5 分

9．已知向量，且向量与垂直，则实数的值是_________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平面向量的坐标运算平面向量数量积的运算量积判断两个平面向量的垂直关系

题型：填空题

填空题 · 5 分

11．设向量满足，则的夹角是_________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平面向量数量积的运算数量积表示两个向量的夹角量积判断两个平面向量的垂直关系

题型：简答题

简答题 · 8 分

27．已知两个向量

（1）若，求实数的值；

（2）求函数的值域。

正确答案

；值域为．

解析

试题分析：本题属于向量和对数函数中的基本问题，题目的难度是逐渐由易到难，

（1）直接按照步骤来求

（2）要注意转化后的定义域．

（1）

经检验为所求的解；

（2）由条件知

所以值域为。

考查方向

本题考查了向量和对数函数的知识

解题思路

本题考查向量和对数函数，解题步骤如下：

1、利用向量垂直化简求解。

2、利用换元法转化为二次函数求解。

易错点

利用换元法时容易出错。

知识点

对数函数的值域与最值平面向量数量积的运算量积判断两个平面向量的垂直关系

继续学习学习下一知识点

下一知识点 : 平面向量数量积坐标表示的应用

百度题库 > 高考 > 理科数学 > 量积判断两个平面向量的垂直关系

扫码查看完整答案与解析