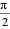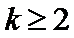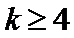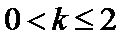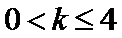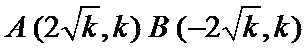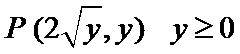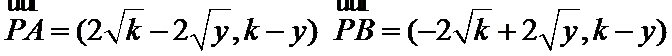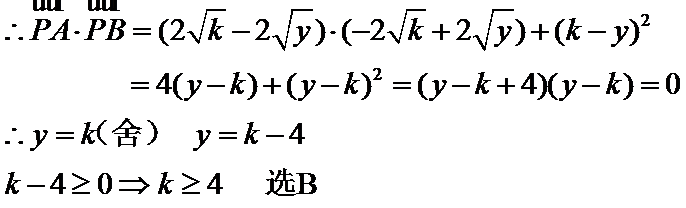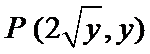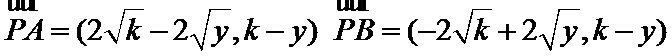- 量积判断两个平面向量的垂直关系
- 共78题
15.已知向量


正确答案
解析
设向量




选项A:
选项B:

选项C:

选项D:由A选项的证明可知







考查方向
本题考查平面向量垂直与平行的条件、向量数量积的运算,是容易题.
解题思路
向量垂直用两个向量的数量积为零来判定,向量平行用向量平行的条件判定.
易错点
混淆平面向量垂直与平行的条件,对充分性和必要性认识不足.
知识点
13.已知


正确答案
2
解析
由已知,
因为
所以
解得
应填2.
考查方向
解题思路
本题主要考查平面向量的坐标运算,向量的垂直等知识。
解题步骤如下:
①由向量垂直的条件,列出方程;
②解出方程,即得答案。
易错点
本题易把向量的平行和垂直的条件混淆,从而出现错误。
知识点
11.在平面直角坐标系



使得

正确答案

解析
设满足条件PA=2PB的P点坐标为(x,y),则(x-4)2+y2=4(x-1)2+4y2,
化简得x2+y2=4.
要使直线x-y+m=0有交点,
则 
即
考查方向
解题思路
本题主要考查直线与圆的位置关系,点到直线距离.
解题步骤如下:由已知条件,求出P点的轨迹方程。利用直线与圆的位置关系解决。
易错点
本题易错点是找不到P点的轨迹是圆,
从而不能利用直线与圆的位置关系解决。
知识点
6.若非零向量




正确答案
解析

又因为

考查方向
解题思路
根据垂直关系得到向量
易错点
向量垂直与向量积的关系
知识点
4.设

正确答案
知识点
已知角







正确答案
解:(1)由

且

∴

∴
(2)由余弦定理得
,而∵
由


当且仅当
又


所以

解析
本题属于三角函数的基本问题,题目的难度是中等,本题的关键是:
(1)、向量的基本运算以及三角函数恒等变换的应用;
(2)、余弦定理与基本不等式之间的应用,一直是考试的热点问题,
考查方向
本题考查了向量运算、三角函数恒等变换、正弦定理和余弦定理的综合应用
易错点
向量的运算、余弦定理的应用,需要注意
知识点
13.向量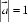
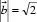
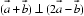

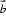
正确答案
解析
由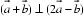
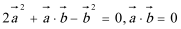

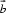
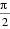
考查方向
本题主要考查了平面向量的夹角公式。
解题思路
本题考查平面向量的夹角公式,解题步骤如下:
1、利用垂直条件求出数量积。
2、利用夹角公式求解.
易错点
本题必须注意数量积的公式。
知识点
13.已知平面直角坐标系中,



正确答案
解析
向量a在向量b的方向上的投影是,
考查方向
向量的数量积的概念.
解题思路
利用向量的数量积性质求解
易错点
向量的在另一个向量上投影的概念理解有误
知识点
12.已知向量



正确答案
解析
考查方向
解题思路
本题主要是突破点在于垂直与数量积之间的转换
易错点
本题注意向量垂直与数量积之间的转换
知识点
10.已知抛物线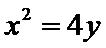
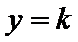
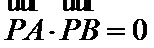
正确答案
解析
抛物线与直线y=k联立确定AB两点的坐标
设动点
则
考查方向
解题思路
本题属于多知识迁移题,需要对知识进行有效转换
(1)确定AB两点的坐标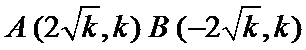
(2)向量
(3)利用向量的数量积运算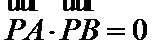
易错点
该题主要易错于题意理解错误,不能有效进行知识的转换
知识点
扫码查看完整答案与解析