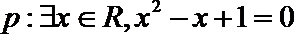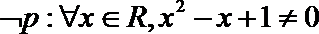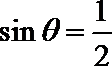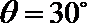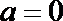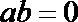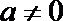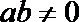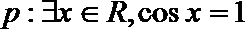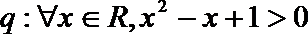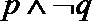- 平行公理
- 共49题
15.若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图所示,在四棱锥



(1)若


(2)点







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知直线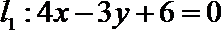
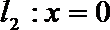
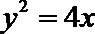
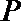
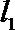
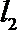
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图:四棱锥P—ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=
(1)证明:无论点E在BC边的何处,都有PE⊥AF;
(2)当BE等于何值时,PA与平面PDE所成角的大小为45°。
正确答案
解:(1)
则P(0,0,1),B(0,1,0),


(2)
解析
解析已在路上飞奔,马上就到!
知识点
19.若函数









(1)已知


(2)试探究是否存在实数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
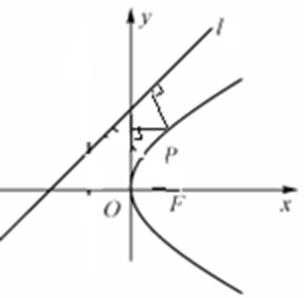
20.在平面直角坐标系中,已知抛物线

(I)求弦长
(II)是否存在平行于y轴的直线l,使得l被以AM为直径的圆所截得的弦长为定值?若存在,求出l的方程;若不存在,说明理由.
正确答案
解:(I)设
直线
①当
②当

得
比较①②知
(II)设存在平行于y轴的直线l,方程为

l被圆C截得的弦长为q,则由圆的几何性质可得:
当

故存在这样的直线l,其方程为
解析
解析已在路上飞奔,马上就到!
知识点
3.下列说法错误的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在







(1)求角
(2)若


正确答案
解:
(1)

(2)由

解析
解析已在路上飞奔,马上就到!
知识点
5.正方形ABCD在平面α内,PB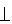
正确答案
解析
∵PB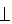
知识点
扫码查看完整答案与解析