- 平行公理
- 共49题
1
题型:简答题
|
如图,三棱柱






(1)求证:
(2)求二面角
(3)在侧棱


正确答案
解析
(1)证明:连接B1C,与BC1相交于O,连接OD。 …………1分
∵BCC1B1是矩形,∴O是B1C的中点。
又D是AC的中点,∴OD//AB1。
∵AB1

(2)解:如图,建立空间直角坐标系,
则C1(0,0,0),B(0,3,2),
C(0,3,0),A(2,3,0),
D(1,3,0),

知识点
平行公理
1
题型:
单选题
|
已知双曲线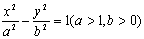
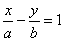
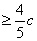
正确答案
A
解析
略
知识点
平行公理
1
题型:填空题
|
平面直角坐标系中,O为原点,A、B、C三点满足

正确答案
解析
略
知识点
平行公理
1
题型:
单选题
|
在整数集









正确答案
C
解析
略
知识点
平行公理
1
题型:简答题
|
如图,在直三棱柱



(1)求三棱柱

(2)求异面直线

正确答案
见解析
解析
(1)在△





所以
(2)连结





在△



由余弦定理,
所以
即异面直线


知识点
平行公理
下一知识点 : 空间图形的公理
扫码查看完整答案与解析