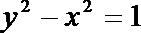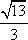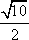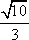直接法求轨迹方程
共25题

· 直接法求轨迹方程

直接法求轨迹方程
共25题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

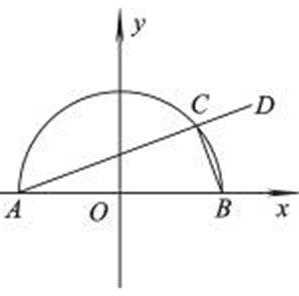
17．如图所示， C是半圆弧x2+y2=1（y≥0）上一点，连接AC并延长至D，使|CD|=|CB|，则当C点在半圆弧上从B点移动至A点时，D点的轨迹是____的一部分，D点所经过的路程为_____

正确答案

圆；

解析

解析已在路上飞奔，马上就到！

知识点

弧长公式二倍角的正切直线的倾斜角与斜率直接法求轨迹方程

题型：简答题

简答题 · 12 分

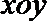
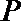
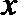
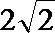
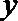
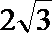
20.在平面直角坐标系中，已知圆在轴上截得线段长为，在轴上截得线段长为.

（I）求圆心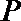的轨迹方程；

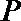
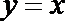
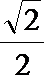
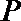
（II）若点到直线的距离为，求圆的方程.

正确答案

（Ⅰ）

（Ⅱ）

解析

解析已在路上飞奔，马上就到！

知识点

点到直线的距离公式圆的标准方程直线与圆相交的性质直接法求轨迹方程

题型：单选题

单选题 · 5 分

6．到椭圆右焦点的距离与到定直线距离相等的动点轨迹方程是（）

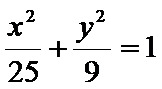
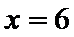
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的标准方程和几何性质直接法求轨迹方程

题型：简答题

简答题 · 13 分

21．已知点和直线，作垂足为Q，且

（Ⅰ）求点P的轨迹方程；

（Ⅱ）过点C的直线m与点P的轨迹交于两点点，若的面积为，求直线的方程．

正确答案

解：（Ⅰ）由已知知．

所以，设，代入上式得

平方整理得．

（Ⅱ）由题意可知设直线的斜率不为零，且恰为双曲线的右焦点，

设直线的方程为，

由

若，则直线与双曲线只有一个交点，这与矛盾，故．

由韦达定理可得

故直线的方程为．

解析

解析已在路上飞奔，马上就到！

知识点

直线的一般式方程双曲线的定义及标准方程直线与圆锥曲线的综合问题直接法求轨迹方程

题型：单选题

单选题 · 5 分

双曲线的离心率为（）

正确答案

解析

略

知识点

直接法求轨迹方程

题型：单选题

单选题 · 5 分

已知为平面内两个定点，过该平面内动点作直线的垂线，垂足为.若，其中为常数，则动点的轨迹不可能是………………（）

A圆

B椭圆

C双曲线

D抛物线

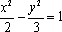
正确答案

解析

略

知识点

直接法求轨迹方程

题型：简答题

简答题 · 14 分

在平面直角坐标系中，点到两点，的距离之和为，设点的轨迹为曲线.

（1）写出的方程；

（2）设过点的斜率为（）的直线与曲线交于不同的两点,，点在轴上，且，求点纵坐标的取值范围.

正确答案

（1）的方程为

（2）

解析

（1）由题设知,

根据椭圆的定义，的轨迹是焦点为，，长轴长为的椭圆，

设其方程为

则，，，所以的方程为. ………5分

（2）依题设直线的方程为.将代入并整理得，

. . ………6分

设，，

则， ..………7分

设的中点为，则，，即. ………8分

因为，

所以直线的垂直平分线的方程为， ……9分

令解得，， .………10分

当时，因为，所以； .………12分

当时，因为，所以. .………13分

综上得点纵坐标的取值范围是. .………14分

知识点

直线与圆锥曲线的综合问题直接法求轨迹方程圆锥曲线中的范围、最值问题

题型：简答题

简答题 · 13 分

已知直角坐标平面内一动点到点的距离与直线的距离相等。

（1）求动点的轨迹的方程；

（2）过点（）作斜率为的直线与曲线相交于两点，若为钝角，求实数的取值范围；

（3）过点（）作直线与曲线相交于两点，问：是否存在一条垂直于轴的直线与以线段为直径的圆始终相切？若存在，求出的值；若不存在，请说明理由。

正确答案

见解析

解析

（1）由抛物线的定义，知所求P点的轨迹是以为焦点，直线为准线的抛物线，其方程为，其中，。

所以，动点P的轨迹C的方程为，………………………………………4分

（2）由题意知，直线AB的方程为。

代入，得。

设，则。

为钝角，。

又，，

。

即，

。

因此，

。

综上，实数的取值范围是，…………………8分

（3）设过点的直线方程为，代入，得

，设，则，。

于是。

的中点坐标为。

又

。

设存在直线满足条件，则。

化简，得。

所以，对任意的恒成立，

所以解得，。

所以，当时，存在直线与以线段为直径的圆始终相切，……13分

知识点

直线与圆锥曲线的综合问题直接法求轨迹方程圆锥曲线中的范围、最值问题圆锥曲线中的探索性问题

题型：单选题

单选题 · 5 分

8．设动点在直线上，为坐标原点，以为直角边，为直角顶点作等腰，则动点的轨迹是（）

A圆

B两条平行直线

C抛物线

D双曲线

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线的一般式方程直接法求轨迹方程

题型：简答题

简答题 · 16 分

18.设函数分别在、处取得极小值、极大值.平面上点A.B的坐标分别为、,.该平面上动点P在圆c：上。

求：

（Ⅰ）点A.B的坐标；

（Ⅱ）求面积的最大值。

正确答案

略

解析

解析已在路上飞奔，马上就到！

知识点

利用导数求函数的极值平面向量数量积的运算直接法求轨迹方程

继续学习学习下一知识点

下一知识点 : 用其它方法求轨迹方程

百度题库 > 高考 > 文科数学 > 直接法求轨迹方程

扫码查看完整答案与解析