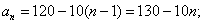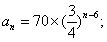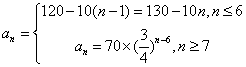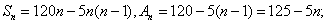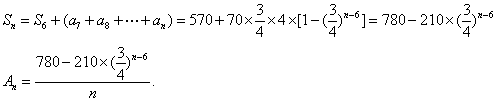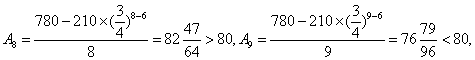- 分段函数模型
- 共10题
19.因发生意外交通事故,一辆货车上的某种液体泄露到一鱼塘中。为治理污染,根据环保部门的建议,现决定在鱼塘中投放一种可与污染液体发生化学反应的药剂。已知每投放



(1)若一次投放4个单位的药剂,则有效治污的时间可达几天?
(2)若因材料紧张,第一次只能投放2个单位的药剂,6天后再投放


正确答案
解:(1)因为 

①当



②当



综合得,
(2) 当


由题意知,

因为


故当且仅当


令



又

解析
解析已在路上飞奔,马上就到!
知识点
21.已知一企业生产某产品的年固定成本为10万元,每生产千件需另投入2.7万元,设该企业年内共生产此种产品

(1)写出年利润

(2)年产量为多少千件时,该企业生产此产品所获年利润最大?(注:年利润=年销售收入-年总成本)
正确答案
(1)当

当

(2)①当




当





②当

当且仅当


综合①、②知

所以为9千件时,该企业生产此产品获利最大.
解析
解析已在路上飞奔,马上就到!
知识点
对任意实数a,b定义运算“



正确答案
解析
略
知识点
某企业在第1年初购买一台价值为120万元的设备M,M的价值在使用过程中逐年减少,从第2年到第6年,每年初M的价值比上年初减少10万元;从第7年开始,每年初M的价值为上年初的75%。
(1)求第n年初M的价值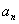
(2)设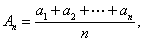
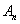
正确答案
见解析
解析
(1)当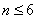
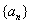
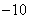
当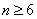
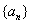
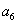
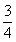
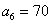
因此,第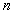
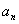
(2)设
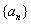
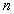
当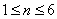
当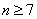
因为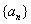
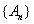
所以须在第9年初对M更新。
知识点
某城市随机抽取一个月(30天)的空气质量指数
(1)根据以上数据估计该城市这30天空气质量指数
(2)若该城市某企业因空气污染每天造成的经济损失


若在本月30天中随机抽取一天,试估计该天经济损失
正确答案
(1)175(2)
解析
解析:(1)该城市这30天空气质量指数

(2)设“在本月30天中随机抽取一天,该天经济损失
由

根据表格数据得共有9+4=13天
所以 
知识点
扫码查看完整答案与解析