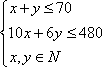- 组合数公式的推导
- 共57题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
若

正确答案
解析
若
则:f(x)=x2﹣2,∴x2﹣2=x2+2



若

则:f(x)=x2﹣






若

则:f(x)=x2+





若
则:f(x)=x2+2,∴x2+2=x2+2



知识点
过点







正确答案

解析
设A(x1,y1),B(x2,y2),则

∵过点M(1,1)作斜率为﹣


∴两式相减可得
∴a=
∴
∴e=

知识点
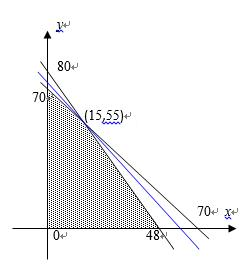
某加工厂用某原料由甲车间加工出A产品,由乙车间加工出B产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克A产品,每千克A产品获利40元,乙车间加工一箱原料需耗费工时6小时可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙两车间耗费工时总和不得超过480小时,甲、乙两车间每天总获利最大的生产计划为
正确答案
解析
设甲车间加工原料x箱,乙车间加工原料y箱
则
目标函数z=280x+300y
结合图象可得:当x=15,y=55时z最大
本题也可以将答案逐项代入检验。
知识点
已知函数f(x)=cosx(sinx+cosx)﹣
(1)若0<α<

(2)求函数f(x)的最小正周期及单调递增区间。
正确答案
(1)∵0<α<

∴cosα=
∴f(α)=cosα(sinα+cosα)﹣
=


=
(2)f(x)=cosx(sinx+cosx)﹣
=sinxcosx+cos2x﹣
=

=

∴T=
由2kπ﹣




∴f(x)的单调递增区间为[kπ﹣

解析
三角函数的图像与性质。
(1)利用同角三角函数关系求得cosα的值,分别代入函数解析式即可求得f(α)的值。
(2)利用两角和公式和二倍角公式对函数解析式进行恒等变换,进而利用三角函数性质和周期公式求得函数最小正周期和单调增区间。
知识点
植树节某班20名同学在一段直线公路一侧植树,每人植一棵,相邻两棵树相距10米,开始时需将树苗集中放置在某一树坑旁边,使每位同学从各自树坑出发前来领取树苗往返所走的路程总和最小,这个最小值为 (米)。
正确答案
2000
解析
(方法一)设树苗放在第
1 2 … 
那么各个树坑到第i个树坑距离的和是




(方法二)根据图形的对称性,树苗放在两端的树坑旁边,所得路程总和相同,取得一个最值;所以从两端的树坑向中间移动时,所得路程总和的变化相同,最后移到第10个和第11个树坑旁时,所得的路程总和达到另一个最值,所以计算两个路程和即可。树苗放在第一个树坑旁,则有路程总和是

知识点
选修4-4:坐标系与参数方程
将圆
(1)写出C的参数方程;
(2)设直线



正确答案
(1)参数方程为 
(2)ρ=
解析
(1)在曲线C上任意取一点(x,y),由题意可得点(x,
∴x2+


(2)由


则线段P1P2的中点坐标为(
再根据与l垂直的直线的斜率为



再根据x=ρcosα、y=ρsinα 可得所求的直线的极坐标方程为ρcosα﹣2ρsinα+
即 ρ=
知识点
在直角坐标系



区域(含边界)上
(1)若

(2)设



正确答案
(1) 
解析
(1)

知识点
有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有( )
正确答案
解析
根据题意,先从6名男医生中选2人,有C62=15种选法,
再从5名女医生中选出1人,有C51=5种选法,
则不同的选法共有15×5=75种;
故选C。
知识点
已知定点A(-1,0),F(2,0),定直线l:x=
(1)求E的方程;
(2)试判断以线段MN为直径的圆是否过点F,并说明理由。
正确答案
见解析
见解析。
解析
知识点
扫码查看完整答案与解析