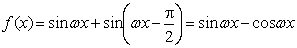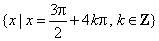1
题型:简答题
|
如图1,在等腰直角三角形











(1) 证明:

(2) 求二面角
正确答案
见解析
解析
(1)在图1中,易得
连结

由翻折不变性可知
所以

理可证



(2) 传统法:过




因为


所以

结合图1可知,






向量法:
以

则

所以
设





由(1) 知,

所以


知识点
弧长公式
1
题型:简答题
|
在△

(1)求角
(2)如果

正确答案
(1)
(2)△
解析
(1)因为

所以

因为

(2)因为

因为



所以
所以△

知识点
弧长公式
1
题型:
单选题
|
已知等差数列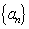
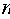
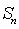
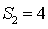
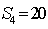
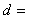
正确答案
B
解析
略
知识点
弧长公式
1
题型:填空题
|
已知


且

于________.
正确答案
解析
略
知识点
弧长公式
1
题型:简答题
|
设函数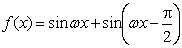
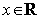
(1)若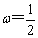
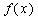
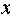
(2)若
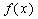
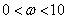
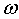
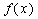
正确答案
见解析。
解析
(1)
当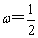
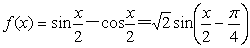
而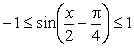
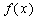
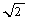
此时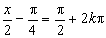
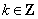
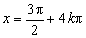
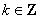
∴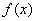
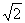
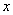
(2)依题意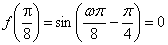
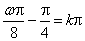
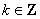
整理,得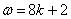
又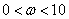
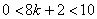

而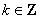
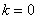
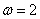
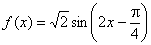
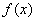
知识点
弧长公式
下一知识点 : 扇形面积公式
扫码查看完整答案与解析