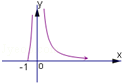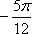- 函数的图象与图象变化
- 共221题
设函数



正确答案
解析
略
知识点
已知函数

正确答案
解析
略
知识点
某企业生产甲.乙两种产品,已知生产每吨甲产品要用A原料3吨.B原料2吨;生产每吨,乙产品要用A原料1吨.B原料3吨,销售每吨甲产品可获得利润1万元,每吨乙产品可获得利润3万元,该企业在某个生产周期内甲产品至少生产1吨,乙产品至少生产2吨,消耗A原料不超过1 3吨,消耗B原料不超过1 8吨,那么该企业在这个生产周期内获得最大利润时甲产品的产量应是
正确答案
解析
略
知识点
记函数


(1)讨论函数
(2)若实数



正确答案
见解析。
解析
(1)由已知得

① 当






所以



② 当


由




所以



此时


(2)由

所以
显然分母
则
所以


又


故当


所以


知识点
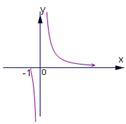
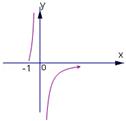
已知函数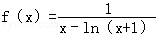
正确答案
解析
令g(x)=x﹣ln(x+1),则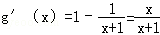
由g'(x)>0,得x>0,即函数g(x)在(0,+∞)上单调递增,
由g'(x)<0得﹣1<x<0,即函数g(x)在(﹣1,0)上单调递减,
所以当x=0时,函数g(x)有最小值,g(x)min=g(0)=0,
于是对任意的x∈(﹣1,0)∪(0,+∞),有g(x)≥0,故排除B、D,
因函数g(x)在(﹣1,0)上单调递减,则函数f(x)在(﹣1,0)上递增,故排除C,
故选A。
知识点
已知
(1)求
(2)判断
(3)若当

正确答案
见解析。
解析
(1)令


∴函数的解析式
(2)

设
则

∴
(3)若当




∴


由

知识点
已知函数

(1)求
(2)设








正确答案
见解析。
解析
(1)

①


②


③

④



(2)由题意
又:



要证

即
令



即

知识点
将函数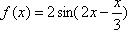
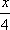
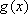
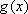
正确答案
解析
略
知识点
已知函数
(1)若

(2)设


正确答案
见解析。
解析
(1)当

(2)当
若

若


当

若


当

当


综上得
知识点
已知函数
(1)求函数
(2)在△





正确答案
见解析。
解析
(1)

∵
∴
∴
∴函数

(2)
∴


在


∴

解得:
∵

知识点
扫码查看完整答案与解析