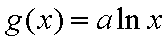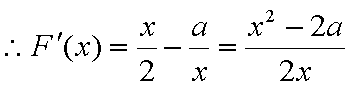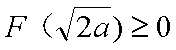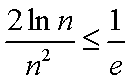- 函数的图象与图象变化
- 共221题
函数y=lg
正确答案
解析
函数的定义域为


知识点
要得到函数

正确答案
解析
知识点
若任意直线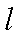
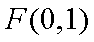
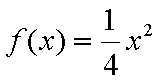
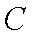
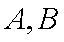
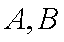
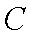
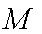
(1)证明:点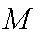
(2)若不等式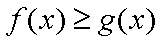

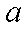
(3)求证: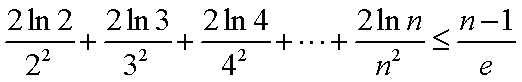
正确答案
见解析。
解析
证明:(1)设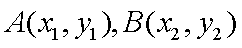
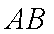

将其代入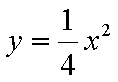
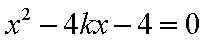
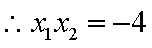
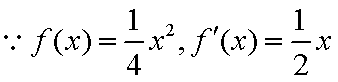
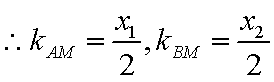
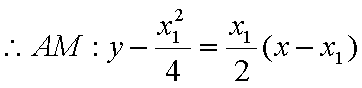
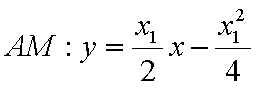
同理: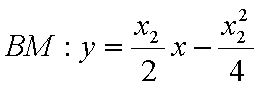
由①②消去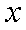
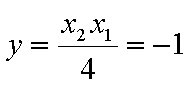
(2)令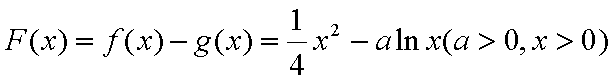
令 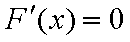
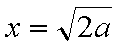
当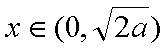
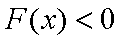
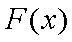
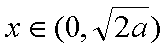
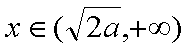
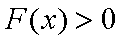
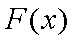
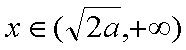
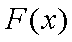
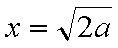
要使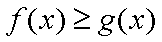
即 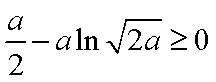
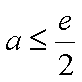
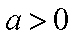
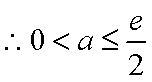
(3)根据(2):取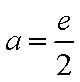
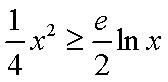
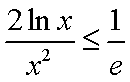
分别令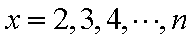
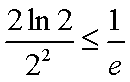
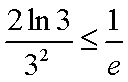
相加: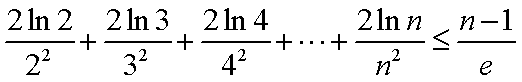
知识点
函数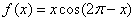
正确答案
解析
因为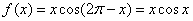
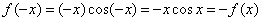
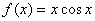
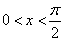
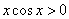
知识点
已知函数






(1)求函数
(2)已知横坐标分别为







正确答案
见解析
解析
(1)由图可知,
最小正周期

又
所以

所以
(2)解法一: 因为

所以

从而
由

解法二: 因为

所以



则
由

知识点
为得到函数






正确答案
解析
由条件可得


知识点
函数
正确答案
解析
函数

知识点
函数f(x)=2cosxsin(x﹣A)+sinA,(x∈R)在x=
(1)求角A的大小;
(2)求函数f(x)在区间[﹣

正确答案
见解析
解析
解:(1)f(x)=2cosxsin(x﹣A)+sinA
=2sinxcosxcosA﹣2cos2xsinA+sinA
=sin2xcosA﹣cos2xsinA
=sin(2x﹣A),
∵f(x)在x=
∴2×

∴A=﹣2kπ+
∵A∈[0,π],∴A=
(2)由(1)知,f(x)=sin(2x﹣
∵x∈[﹣

∴(2x﹣


∴f(x)在区间[﹣


知识点
函数f(x)=sin(


正确答案
解析
由图可知函数的周期为:T=






所以,f(x)=



知识点
函数y=

正确答案
解析
当



知识点
扫码查看完整答案与解析