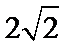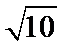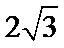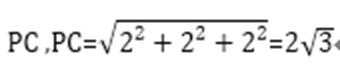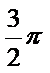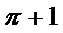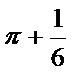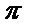- 由三视图还原实物图
- 共40题
9.如图是正三棱锥V-ABC的正视图、侧视图和俯视图,则其侧视图的面积是
正确答案
解析
如图计算底面高
体高
所以侧面积
考查方向
解题思路
1)根据三视图得出底边长为
2)计算体高VA,得出结果
易错点
主要易错于读错数据
知识点
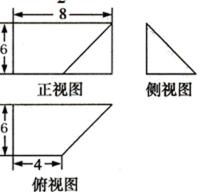
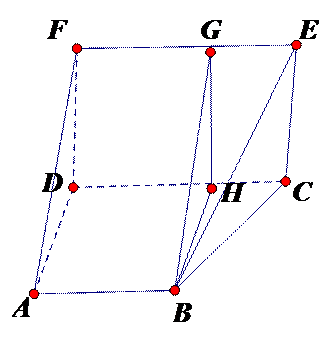
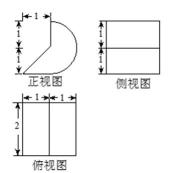
5.高为4的直三棱柱被削去一部分后得到一个几何体,它的直观图和三视图中的侧视图、俯视图如图所示,则该几何体的体积是原直三棱柱的体积的( )
正确答案
解析
根据三视图可知直观图为:放倒的四棱锥,
∵底面是直角梯形,且上底为4,下底为2,梯高2
∴
∴
又因为

考查方向
解题思路
1)根据直观图形状:放倒的四棱锥,底面是直角梯形,
2)读取几何图形的数据
易错点
主要出现在两个地方:①不能得到直观图为四棱锥,②直观图读取直观图数据错误,特别是底面上的长宽数据
知识点
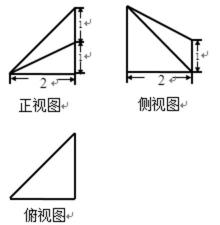
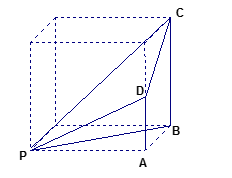
3.如图,某多面体的三视图中正视图、侧视图和俯视图的外轮廓分别为直角三角形、直角梯形和直角三角形,则该多面体的各条棱中,最长的棱的长度为
正确答案
解析
多面体的直观图如图所示,根据多面体的特点,最长的棱长为
考查方向
解题思路
直接画出直观图,有直观图求出最长的棱
易错点
识图不准,画错直观图
知识点
10.如图,网格纸上小正方形的边长为
正确答案
解析
根据三视图还原成几何体如图所示,该四面体的表面积为
因此A选项不正确,C选项不正确,D选项不正确,所以选B选项。
考查方向
解题思路
根据三视图还原几何体为一个三棱锥,由图中数据可算出该四面体的表面积。
易错点
不能通过左视图中的虚线(实线)构想出其中一个顶点的位置而出错。
知识点
9.某几何体的三视图如图所示, 则该几何体的体积为______,表面积为______.
正确答案

解析
由三视图可知几何体为圆锥的 ,底面半径为1,高为2.母线为
∴几何体的体积
几何体的表面积
故答案为 
考查方向
解题思路
还原直观图可知是圆锥的一半,所以体积为圆锥的一半,求面积要注意截面
易错点
主要易错于三视图数据读取错误,忽视截面的面积
知识点
9.某空间几何体的三视图如图所示,则该几何体的外接球的表面积是( )
正确答案
解析
由三视图可知,该几何体为直三棱柱,高为4,底面为等腰三角形,底长为



考查方向
解题思路
1.先根据三视图还原原来的几何体;2.找到几何体外接球的球心在中界面的外心处,然后利用几何图形求解。
易错点
1.不能根据三视图还原原来的几何体;2.不会确定几何体外接球的球心在什么位置。
知识点
9.若某几何体的三视

正确答案
解析
该几何体是三棱柱



考查方向
解题思路
1.先根据三视图还原成原来的几何体为三棱柱


易错点
1.不会根据三视图还原原来的几何体形状;2.不知道如何求不规则的几何体的体积导致割补出错。
知识点
5.一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是
正确答案
解析
由三视图,可知该几何体的直观图如图所示,取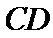
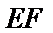
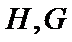
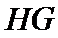
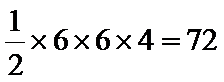
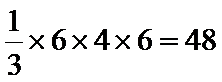
考查方向
解题思路
1)根据几何体的三视图,画出该几何体的直观图;
2) 分割几何体,分别判定几何体形状求其体积;
3)求和,即得该几何体的体积。
易错点
本题易在分割几何体时出现错误,而且求锥体的体积忘记乘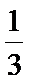
知识点
10.一个几何体由多面体和旋转体的整体或一部分组合而成,其三视图如图所示,则该几何体的体积是( )
正确答案
解析
由三视图可得原几何体是由一个半圆柱和一个三棱锥组合而成,圆柱的底面半径为1,高位2,所以体积为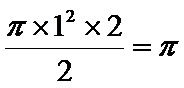
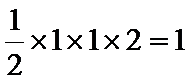
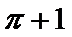
考查方向
解题思路
1)根据几何体的三视图,画出该几何体的直观图;
2)分割几何体,分别判定几何体形状求其体积;
3)求和,即得该几何体的体积。
易错点
本题易在由三视图得到直观图时发生错误,导致体积求错。
知识点
12.如图,是一个几何体的三视图,其中正视图与侧视图完全相同,均为等边三角形与矩形的组合,俯视图为圆,若已知该几何体的表面积为

正确答案
解析
由该几何体的三视图可知,几何体上面是一个圆锥,下面是一个圆柱,所以

考查方向
解题思路
1.先根据三视图判断出原来的几何体的形状;2.利用求表面积的公式解方程即可。
易错点
1.不会根据三视图还原原来的几何体;2.不会计算该几何体的体积。
知识点
扫码查看完整答案与解析