- 一元二次不等式的解法
- 共69题
11.设f(x)是定义在R上且周期为2的函数,在区间[ −1,1)上,


正确答案
知识点
13.设x,y满足约束条件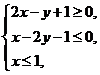
正确答案
知识点
1.若不等式(a-1)x2+(a-1)x+1>0恒成立,则a的取值范围为( )
正确答案
解析
(1)若a=1,可以看出不等式(a-1)x2+(a-1)x+1>0恒成立.
(2)若a≠1,欲使不等式(a-1)x2+(a-1)x+1>0恒成立,
则

综合(1)(2),得a的取值范围为{a|a=1或a>5}.
知识点
5.已知命题p:方程a2x2+ax-2=0在[-1,1]上有解;命题q:只有一个实数x满足不等式x2+2ax+2a≤0。若命题“p∨q”为假命题,则实数a的取值范围是( )
正确答案
解析
若命题“p∨q”为假命题,则p假且q假.
当p假时,令f(x)=a2x2+ax-2,则方程a2x2+ax-2=0在[-1,1]上无解
∴a=0或
故a∈(-1,1).
当q假时,Δ=4a2-8a≠0∴a≠0,a≠2.
综上,a∈(-1,0)∪(0,1).故选B.
知识点
1.不等式ax2+bx+c>0(c≠0)的解集一定不可能是( )
正确答案
解析
当a>0且b2-4ac<0时,解集为R
当a<0且b2-4ac<0时,解集为⌀
当a=0且b≠0时,解集为{x|x>-
无论哪种情况,选项D中的解集都不可能出现.
知识点
1.若不等式(a-1)x2+(a-1)x+1>0恒成立,则a的取值范围为( )
正确答案
解析
(1)若a=1,可以看出不等式(a-1)x2+(a-1)x+1>0恒成立.
(2)若a≠1,欲使不等式(a-1)x2+(a-1)x+1>0恒成立,
则

综合(1)(2),得a的取值范围为{a|a=1或a>5}.
知识点
4.已知函数f(x)=
正确答案
解析
f(x)=
由f(x)的图象(图略)可知f(x)在R上是单调递增函数
由f(2-a2)>f(a),得2-a2>a
即a2+a-2<0,解得-2<a<1.
知识点
6.直线y=k(x+1)(k∈R)与不等式组
正确答案
解析
不等式组表示的平面区域如图所示,直线y=k(x+1)(k∈R)恒过定点(-1,0)当直线y=k(x+1)过点A时,k最大为2;当直线y=k(x+1)过点B时,k最小为-2,所以k的取值范围是[-2,2] ,故选(A)
考查方向
解题思路
先画出不等式组表示的平面区域,由直线的解析式可知,直线经过定点(-1,0),根据斜率k的几何意义即可求出k的取值范围。
易错点
1、本题易在画平面区域时发生错误 。2、本题不容易理解直线过的定点坐标是(-1,0)甚至有些学生不知道斜率k的意义,得不到k的最大值为2,最小值为-2,导致题目无法进行。
知识点
11.函数

正确答案
a≥-1
解析
由图可知:a≥-1。
考查方向
解题思路
本题考查函数的图像性质,解题思路如下:
1、画出函数f(x)的图像及y=x的图像;
2、比较函数值的大小。
易错点
本题必须注意单调性的比较
知识点
1.已知集合
正确答案
解析
本题考查了一元二次不等式的解法、对数函数定义域求法、集合的交集与补集运算.解不等式x2-x-2<0,得-1<x<2,所以A=(-1,2),又因为1-|x|>0,解得-1<x<1,所以B=(-1,1),所以


考查方向
本题主要考查了集合的交集与补集运算,是基础题,是高考必考题型之一,常与求不等式的解集,函数的定义域、值域等知识点交汇命题,体现了学生对基础知识的掌握能力。
易错点
本题易在求对数函数的定义域中发生错误.
知识点
扫码查看完整答案与解析