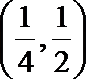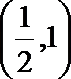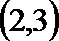导数的运算
共219题

· 导数的运算

导数的运算
共219题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

10．已知函数是定义在R上的可导函数，其导函数记为，若对于任意实数x，有，且为奇函数，则不等式的解集为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数奇偶性的性质导数的运算其它不等式的解法

题型：单选题

单选题 · 5 分

4．若，则下列不等式成立的是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算

题型：填空题

填空题 · 4 分

15．给出以下四个命题：

①命题；命题.则命题“且”是真命题；

②求函数的零点个数为3；

③函数（且）与函数（且）的定义域相同；

④函数是奇函数．

其中不正确的命题序号是__________（把你认为不正确的命题序号都填上）．

正确答案

②

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算

题型：单选题

单选题 · 5 分

11．下图是函数的部分图像，则函数的零点所在的区间是（）

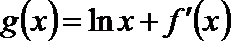
正确答案

解析

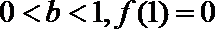
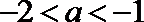
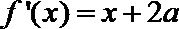
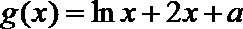
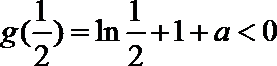
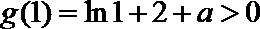
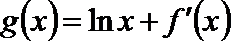
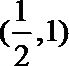
由函数图象可知，从而，，所以，函数在定义域内单调递增，，，所以函数的零点所在的区间是，选C．

知识点

函数零点的判断和求解导数的运算

题型：简答题

简答题 · 14 分

20. 将这个数随机排成一列，得到的一列数称为的一个排列.

定义为排列的波动强度.

（Ⅰ）当时，写出排列的所有可能情况及所对应的波动强度；

（Ⅱ）当时，求的最大值，并指出所对应的一个排列；

（Ⅲ）当时，在一个排列中交换相邻两数的位置称为一次调整，若要求每次调整时波动强度不增加，问对任意排列，是否一定可以经过有限次调整使其波动强度降为9；若可以，给出调整方案，若不可以，请给出反例并加以说明.

正确答案

（Ⅰ）时，排列的所有可能为；；；；；

；；；

；；.

（Ⅱ）

上式转化为，

在上述个中，有个选正号，个选负号，其中出现一次，各出现两次.

所以可以表示为个数的和减去个数的和的形式，

若使最大，应使第一个和最大，第二个和最小.

所以最大为：

所对应的一个排列为：.（其他正确的排列同等给分）

（Ⅲ）不可以.

例如排列，除调整外，其它调整都将使波动强度增加，调整波动强度不变.

所以只能将排列调整为排列.

对于排列，仍然是除调整外，其它调整都将使波动强度增加，所以仍只能调整两个数字.

如此不断循环下去，不可能经过有限次调整使其波动强度降为.

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算

继续学习学习下一知识点

下一知识点 : 导数的加法与减法法则

百度题库 > 高考 > 理科数学 > 导数的运算

扫码查看完整答案与解析