- 导数的运算
- 共219题
12.函数

正确答案
解析
首先构造两个函数


(1)当

(2)当

(3)当



考查方向
解题思路
首先构造两个函数


易错点
1、忽略对数函数的定义域导致结果出错
2、没有注意到后面的二次函数过原点,而增加不必要的讨论和计算
知识点
21. 已知函数
(Ⅰ)设函数

(Ⅱ)若不等式


正确答案
见解析
解析
(Ⅱ)
①当


令




②当



综上,当



当

(Ⅱ)由题意可知,不等式

即在[1,e]存在

由(Ⅰ)中

即函数
由(Ⅰ)知,当

当
①当


②当



③当






综上可得,实数

考查方向
解题思路
确定函数的定义域,利用导数求函数的单调区间,根据题意构造出恰当的不等式,进而求出参数的取值范围。
易错点
求导错误,构造函数不成功。
知识点
12.已知函数


正确答案
解析
由题意得,函数在f(x)在x=1处取到最小值。










令








即
考查方向
解题思路
先判断函数的单调性,然后求导求最值。
易错点
函数单调性判断错误、求导错误
知识点
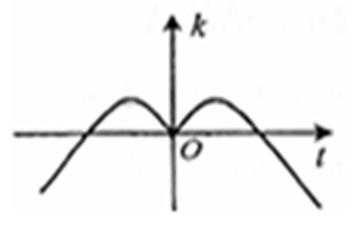
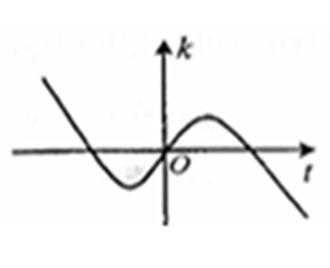
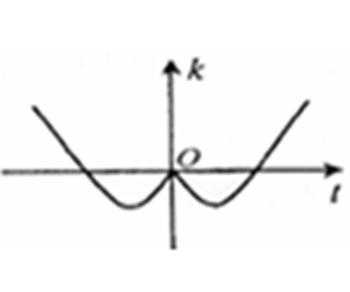
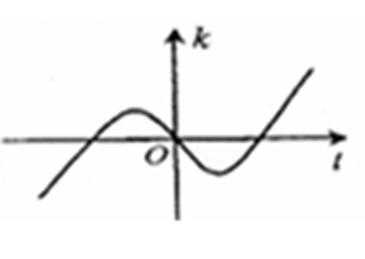
8. 设函数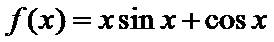
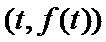
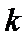
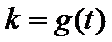
正确答案
解析
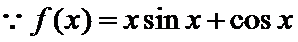
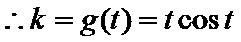
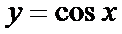
考查方向
解题思路
先求导数,然后利用导函数求k的解析式,进而判断函数图象
易错点
求导错误,函数单调性不会判断
知识点
12.函数




正确答案
解析
由



所以函数

而不等式

所以

考查方向
解题思路
1、先通过题中

2、将题中不等式


易错点
1、不会通过

2、忽视题中函数
知识点
扫码查看完整答案与解析