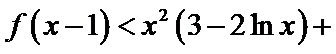导数的运算
共219题

· 导数的运算

导数的运算
共219题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 13 分

设函数.

25.讨论函数在内的单调性并判断有无极值，有极值时求出极值；

26.记，求函数在上的最大值D；

27.在（Ⅱ）中，取，求满足时的最大值.

第(1)小题正确答案及相关解析

正确答案

（Ⅰ）极小值为

解析

（Ⅰ），.

，.

因为，所以.

①当时，函数单调递增，无极值.

②当时，函数单调递减，无极值.

③当，在内存在唯一的，使得.

时，函数单调递减；时，函数单调递增.

因此，，时，函数在处有极小值.

考查方向

1.函数的单调性、极值与最值；2.绝对值不等式的应用.

解题思路

（Ⅰ）将代入为，.

求导得，.因为，所以.按的范围分三种情况进行讨论：①当时，函数单调递增，无极值.②当时，函数单调递减，无极值.③当，在内存在唯一的，使得.时，函数单调递减；时，函数单调递增.因此，，时，函数在处有极小值.

易错点

函数求导错误，分类讨论能力弱，计算能力弱

第(2)小题正确答案及相关解析

正确答案

解析

：

（Ⅱ）时，，

当时，取，等号成立，

由此可知，函数在上的最大值为.

考查方向

1.函数的单调性、极值与最值；2.绝对值不等式的应用.

解题思路

当时，依据绝对值不等式可知，从而能够得出函数在上的最大值为.

易错点

绝对值不等式性质运用错误，计算错误，不会合理放缩不等式

第(3)小题正确答案及相关解析

正确答案

（Ⅲ）1.

解析

（Ⅲ），即，此时，从而.

取，则，并且.

由此可知，满足条件的最大值为1.

考查方向

1.函数的单调性、极值与最值；2.绝对值不等式的应用.

解题思路

（Ⅲ）当，即，此时，从而.依据式子特征取，则，并且.由此可知，满足条件的最大值为1

易错点

平均值不等式的性质，计算能力弱

题型：简答题

简答题 · 5 分

9.定义在区间[0,3π]上的函数y=sin2x的图象与y=cosx的图象的交点个数是 .

正确答案

知识点

导数的运算

题型：填空题

填空题 · 12 分

（本小题满分12分）

(I)讨论函数的单调性，并证明当 >0时，

(II)证明：当时，函数有最小值.设g（x）的最小值为，求函数的值域.

正确答案

（Ⅰ）的定义域为.

且仅当时，，所以在单调递增，

因此当时，

所以

（II）

由（I）知，单调递增，对任意

因此，存在唯一使得即，

当时，单调递减；

当时，单调递增.

因此在处取得最小值，最小值为

于是，由单调递增

所以，由得

因为单调递增，对任意存在唯一的

使得所以的值域是

综上，当时，有，的值域是

知识点

函数的值域函数单调性的判断与证明函数的最值及其几何意义导数的运算

题型：单选题

单选题 · 5 分

10.已知R上的奇函数满足，则不等式的解集是（）

正确答案

解析

设

则，

设，则，由＞0得x＞1，由＜0得0＜x＜1，即当x=1时，函数取得极小值同时也是最小值h（1）=2，

∵，h（x）≥2，∴＞-2+2=0，

即＞0，即在（0，+∞）上为增函数，则当x=1时，

则不等式等价为＜0，即＜

则x＜1，即不等式的解集是（0，1），

∴所以选项B为正确选项

考查方向

本题主要考查了导数的综合应用,属于难题，是高考的热点

解题思路

构造函数g（x），求函数的导数，判断函数的单调性，利用函数的单调性进行求解即可．

易错点

构造函数g（x）错误

知识点

函数奇偶性的性质导数的运算其它不等式的解法

题型：简答题

简答题 · 14 分

设函数，的定义域均为，且是奇函数，是偶函数，，其中e为自然对数的底数.

24.求，的解析式，并证明：当时，，；

25.设，，证明：当时，.

第(1)小题正确答案及相关解析

正确答案

（Ⅰ），.证明：当时，，，故

又由基本不等式，有，即

解析

（Ⅰ）由, 的奇偶性及,①得： ②

联立①②解得，.

当时，，，故 ③

又由基本不等式，有，即 ④

考查方向

1、导数在研究函数的单调性与极值中的应用；

解题思路

（Ⅰ）将等式中用来替换，并结合已知是奇函数，是偶函数可得于是联立方程组即可求出的表达式；当时，由指数与指数函数的性质知，，进而可得到然后再由基本不等式即可得出

易错点

导函数计算出错。

第(2)小题正确答案及相关解析

正确答案

（Ⅱ）由（Ⅰ）得

⑤⑥

当时，等价于 ⑦ 等价于

⑧于是设函数，由⑤⑥，有

当时，（1）若，由③④，得，故在上为增函数，从而，即，故⑦成立.（2）若，由③④，得，故在上为减函数，从而，即，故⑧成立.综合⑦⑧，得 .

解析

（Ⅱ）由（Ⅰ）得， ⑤

， ⑥

当时，等价于， ⑦

等价于 ⑧

设函数，由⑤⑥，有

当时，（1）若，由③④，得，故在上为增函数，从而，即，故⑦成立.（2）若，由③④，得，故在上为减函数，从而，即，故⑧成立.综合⑦⑧，得 .

考查方向

函数的基本性质；

解题思路

（Ⅱ）由（Ⅰ）得，.于是要证明，即证，也就是证明，即证于是构造函数，利用导数在函数的单调性与极值中的应用即可得出结论成立.

易错点

计算量大。

继续学习学习下一知识点

下一知识点 : 导数的加法与减法法则

百度题库 > 高考 > 理科数学 > 导数的运算

扫码查看完整答案与解析