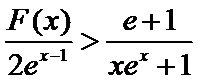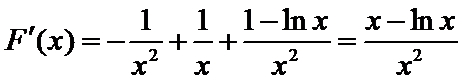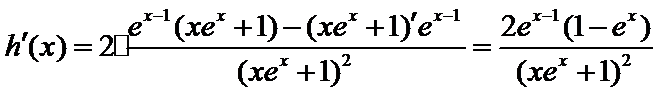- 导数的运算
- 共219题
已知函数
26.若


27.讨论
28.证明:
正确答案
见解析
解析




考查方向
解题思路
先根据导数的性质求切线的斜率,进而求出参数的值,得到函数的解析式,利用导数的性质作出函数大致图像,结合图像,利用分类讨论思想求f(x)的单调性,通过构造适当的函数,进而证明不等式
易错点
求导错误,函数性质理解错误;分类讨论有重有漏
正确答案
见解析
解析
1)若


2)若

3)若
再令
在
综上所述,若
若

若
考查方向
解题思路
先根据导数的性质求切线的斜率,进而求出参数的值,得到函数的解析式,利用导数的性质作出函数大致图像,结合图像,利用分类讨论思想求f(x)的单调性,通过构造适当的函数,进而证明不等式
正确答案
见解析
解析
由27题知,当
当
考查方向
解题思路
先根据导数的性质求切线的斜率,进而求出参数的值,得到函数的解析式,利用导数的性质作出函数大致图像,结合图像,利用分类讨论思想求f(x)的单调性,通过构造适当的函数,进而证明不等式
易错点
求导错误,函数性质理解错误;分类讨论有重有漏
设函数f(x)=ex-ax-2.
27.求f(x)的单调区间;
28.若a=1,k为整数,且当x>0时,(x-k)f′(x)+x+1>0恒成立,求k的最大值.
正确答案
当a≤0时,f(x)的单调递增区间为(-∞,+∞);当a>0时,f(x)的单调递减区间为(-∞,ln a),单调递增区间为(ln a,+∞)
解析
函数f(x)的定义域为(-∞,+∞),f′(x)=ex-a.……1分
当a≤0时,f′(x)>0,所以f(x)在区间(-∞,+∞)上单调递增;
……………………………………3分
当a>0时,若x∈(-∞,ln a),则f′(x)<0,若x∈(ln a,+∞),则f′(x)>0,
所以f(x)在区间(-∞,ln a)上单调递减,在区间(ln a,+∞)上单调递增.
……………………………………5分
综上可知,当a≤0时,f(x)的单调递增区间为(-∞,+∞);当a>0时,f(x)的单调递减区间为(-∞,ln a),单调递增区间为(ln a,+∞)……………………………………6分
考查方向
解题思路
先求导,根据导数的函数特点对,常数a进行合理讨论a小于等于零a大于零两种情况讨论
易错点
分类讨论不全,或者对含有参数的单调性讨论思路不清;
正确答案
k=2
解析
由于a=1,所以(x-k)f′(x)+x+1=(x-k)(ex-1)+x+1.
设g(x)=(x-k)(ex-1)+x+1,则g′(x)=ex(x-k+1).……………………………………7分
(i)若k≤1,则当x>0时,g′(x)>0,所以g(x)在区间(0,+∞)上单调递增,而g(0)=1,
故当x>0时,g(x)>1>0,即有(x-k)f′(x)+x+1>0恒成立.…………………………………9分
(ii)若k>1,则当x∈(0,k-1)时,g′(x)<0;当x∈(k-1,+∞)时,g′(x)>0.
所以g(x)在区间(0,+∞)内的最小值为g(k-1)=k-ek-1+1.………………………………11分
令h(k)=k-ek-1+1,则h′(k)=1-ek-1,因为k>1,所以h′(k)<0,故h(k)在区间(1,+∞)上单调递减.而h(2)>0,h(3)<0,所以当1<k≤2时,h(k)>0,即g(k-1)>0,从而当x>0时,g(x)>0,即(x-k)f′(x)+x+1>0恒成立;当k≥3时,h(k)<0,即g(k-1)<0,故g(x)>0在区间(0,+∞)内不恒成立.……………………………………13分
综上所述,整数k的最大值为2……………………………………14分
考查方向
解题思路
将a=1及导数代入得,g(x)=(x-k)(ex-1)+x+1,则g′(x)=ex(x-k+1).设


易错点
处理逻辑推理与运算求解能力方面易出错。思路不清晰,步骤不严谨
已知函数

26.若曲线



27.若



28.若


正确答案
(1)
解析
(1)当



考查方向
解题思路
1)第一问由


2)第二问由零点的概念,化简函数


3)由



易错点
求导函数,求极值,参数m的讨论是本题的易错点,
正确答案
(2)
解析
(2)由题意,

令
又
∴

∴
∴
∴
考查方向
解题思路
1)第一问由


2)第二问由零点的概念,化简函数


3)由



易错点
求导函数,求极值,参数m的讨论是本题的易错点,
正确答案
(3)综上,当





解析
(3)由

令


∴


∴
又令

令

∴


又
∴当

∴
同理,当



综上,当
当

当

考查方向
解题思路
1)第一问由


2)第二问由零点的概念,化简函数


3)由



易错点
求导函数,求极值,参数m的讨论是本题的易错点,
函数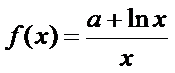

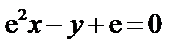

25.若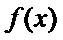
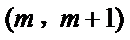


26.求证:当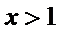
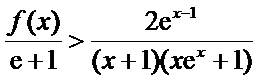
正确答案
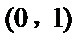
解析
因为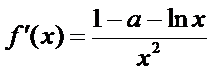
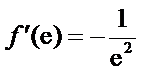
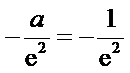
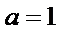
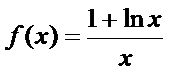
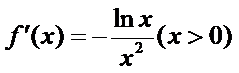
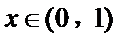
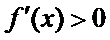
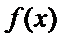
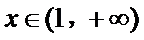
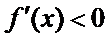
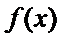
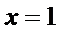
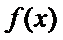
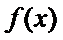
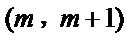
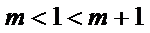
即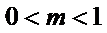
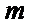
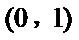
考查方向
解题思路
第一问由切线与直线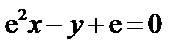
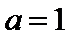
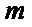
正确答案
略;
解析
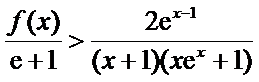
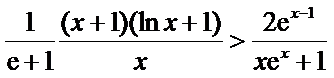
令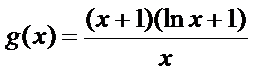
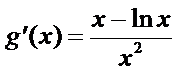
再令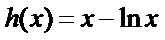
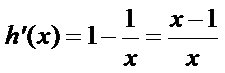
因为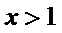
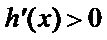
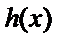
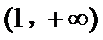
所以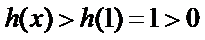
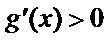
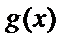
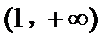
所以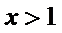
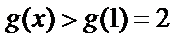

令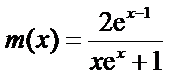

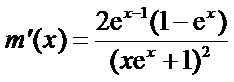
因为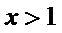
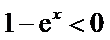
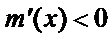
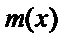
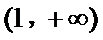
所以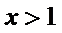
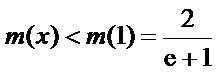
所以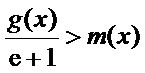
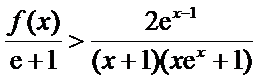
考查方向
解题思路
第二问现将不等式等级变形,构造新函数,对新函数用导函数求最值
12.已知函数





正确答案
解析


(1)当



(2)当













考查方向
解题思路
1.先求导后判断导数的正负,2.当导数有正有负时转化为一元二次方程根的分布处理,接着转化为线性规划使得问题得以解决。
易错点
1.不知道题中的条件:函数



知识点
已知函数
25.讨论
26.当





正确答案
(1)当






解析
(Ⅰ)函数


当



当





当


∴当






考查方向
解题思路
求导后根据a的范围讨论单调性即可;
易错点
问题中不讨论a的范围导致丢解;
正确答案
(2)
解析
(Ⅱ)当











则

由

记


记

∴



而




∴


而





考查方向
解题思路
先利用第(1)问的结论构造函数

易错点
不会构造函数
21.已知函数
(I)若函数


(II)证明:
(III)若不等式

正确答案
见解析
解析
考查方向
解题思路
本题解题思路
1)根据共同的切线的理解得到该点处导函数值与函数值都相等得到t
2)利用单调性确定绝对值内的正负,去掉绝对值号,利用
3)构造关于m的一次函数,把x当作参数消掉m后再使用恒成立问题的解答得出结果
易错点
本题易错在以下几个方面
1)对共同的切线理解不足,第一问出错
2)不能有效去掉绝对值,使用错的解题思想
3)变量间关系不能有效理清
知识点
已知函数f (x)= 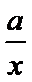
25.若函数f(x)在区间[1,e]上的最小值是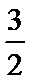
26.当a=1时,设F(x)=f(x)+1+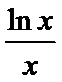
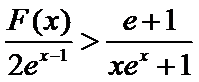
正确答案
(1)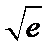
解析
(1)因 为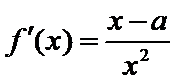
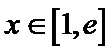
①当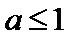
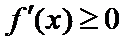
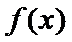
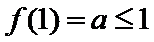
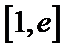
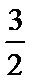
②当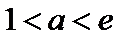
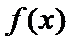
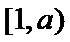
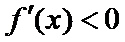
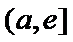
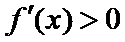
∴函数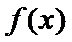
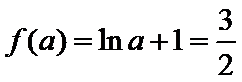
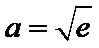
③当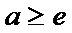
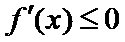
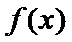
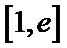
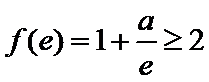
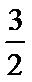
综上所述,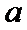
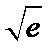
考查方向
解题思路
(1)先对函数进行求导,再对参数进行分类讨论探讨函数的单调性从而研究其最小值及此时a的值 ;(2)通过灵活变形构造新函数的方法证明不等式。
易错点
对参数的分类讨论研究函数的最值。
正确答案
(2)当x>l时,
解析
(2)要证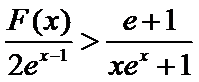
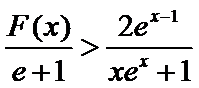
当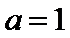
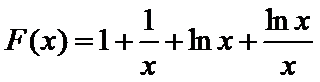
令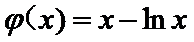
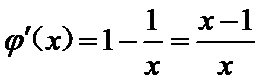
当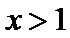
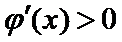
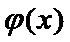
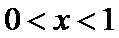
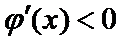
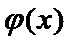
∴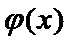
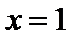
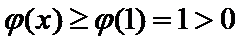
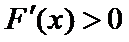
∴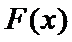
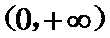
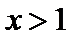
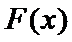
故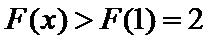
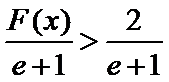
令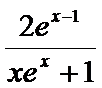
∵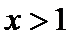
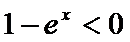
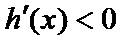
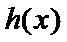
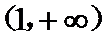
∴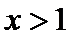
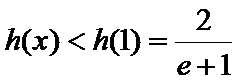
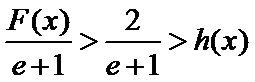
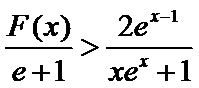
所以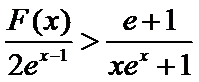
考查方向
解题思路
(1)先对函数进行求导,再对参数进行分类讨论探讨函数的单调性从而研究其最小值及此时a的值 ;(2)通过灵活变形构造新函数的方法证明不等式。
易错点
对参数的分类讨论研究函数的最值。
已知函数
27. 判断函数

28. 若

29.求证:
正确答案
(1)
解析
(Ⅰ)


考查方向
解题思路
直接求导后判断出
易错点
导后的函数不会变形为
正确答案
3;
解析
(Ⅱ)


令

又



当


∴

考查方向
解题思路
先分离参数后变为

易错点
无
正确答案
(3)略
解析
(Ⅲ)由(Ⅱ)知

令
∴
∴
考查方向
解题思路
根据第(2)问放缩
易错点
不会利用放缩法得到
设函数
26.若


27.当

28.若


正确答案
(1)
解析
(Ⅰ)若


得
考查方向
解题思路
根据导数的几何意义求解,
易错点
不清楚
正确答案
(2)


解析
(Ⅱ)由
当

当


由表可知:


所以,当


考查方向
解题思路
先求导,然后判断单调性后即可得到单调区间;
易错点
不清楚
正确答案
(3)略
解析
(Ⅲ)当

令
由指数函数及幂函数的性质知:

又




设


由
当


当


所以当
又
考查方向
解题思路
先将要求的函数变形为
易错点
不会构造函数解决问题,当所要的函数正负不确定时,不知道应该设零点解决。
扫码查看完整答案与解析