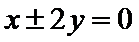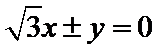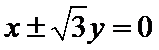抛物线的标准方程和几何性质
共238题

· 抛物线的标准方程和几何性质

抛物线的标准方程和几何性质
共238题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

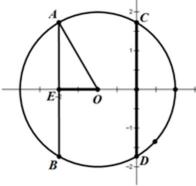
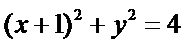
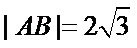
15．已知圆与抛物线的准线交于A、B两点，且，则m的值为__________。

正确答案

解析

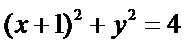
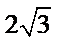
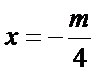
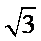
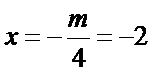
在平面直角坐标系中画出圆如图所示，据图可以知道CD=，因此抛物线的开口是向右的，其准线为．由AE=，OA＝２，得OE=1，因此准线，解得m=8。

考查方向

本题主要考查了抛物线的性质以及直线与圆的位置关系问题，同时考查了学生的数形结合以及分类讨论思想。

解题思路

根据题意画出合适的图形，然后结合图形进行分析和计算．

易错点

本题必须要对抛物线的标准方程和几何性质有深刻的认识，否则容易因为误认为准线为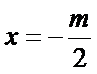而出错。

知识点

抛物线的标准方程和几何性质直线、圆及圆锥曲线的交汇问题

题型：简答题

简答题 · 12 分

20. 已知F（，0）为抛物线（p＞0）的焦点，点N（，）（＞0）为其上一点，点M与点N关于x轴对称，直线与抛物线交于异于M，N的A，B两点，且|NF|=，。

（Ⅰ）求抛物线方程和N点坐标；

（Ⅱ）判断直线中，是否存在使得面积最小的直线，若存在，求出直线的方程和面积的最小值；若不存在，说明理由．

正确答案

见解析

解析

（Ⅰ）由题意，则，

故抛物线方程为。

由|NF|=，则。

∵，

∴，

所以N（2,2）。

（Ⅱ）由题意知直线的斜率不为0，则可设直线的方程为。

联立方程组，得。

设两个交点A（，），B（，）（≠±2，≠±2），则

由，整理得

。

此时，恒成立。

故直线的方程可化为，从而直线过定点E（3，-2）。

因为M（2，-2），

所以M,E所在直线平行x轴，

所以△MAB的面积当t=-2时有最小值为，此时直线的方程为。

考查方向

抛物线的性质与特征，圆锥曲线中的最值问题

解题思路

建立适当的坐标系，利用直线斜率之间的关系建立方程，进而求解，与抛物线联立成方程组，整理可得。

易错点

计算能力弱，找不到面积最小时候的情况

知识点

抛物线的标准方程和几何性质圆锥曲线中的范围、最值问题圆锥曲线中的探索性问题

题型：填空题

填空题 · 4 分

5．抛物线（）上的动点到焦点的距离的最小值为，则_________．

正确答案

解析

知识点

抛物线的标准方程和几何性质

题型：单选题

单选题 · 3 分

5. A（，1）为抛物线x2=2py(p>0)上一点，则A到其焦点F的距离为

B+

D+1

正确答案

解析

将A（，1）代入抛物线x2=2py(p>0)，求得p=1，因为抛物线焦点在y轴上，所以A到其焦点F的距离为，故选A。

考查方向

本题主要考查了抛物线方程及点到焦点的距离。

解题思路

线将A点坐标代入抛物线x2=2py(p>0)，求得p值，再结合点到焦点的距离公式求得。

易错点

由抛物线的标准方程没搞清焦点位置，以至于点到焦点的距离公式用错。

知识点

抛物线的标准方程和几何性质

题型：单选题

单选题 · 5 分

6．已知双曲线与抛物线的一个交点为，为抛物线的焦点，若，则双曲线的渐近线方程（）

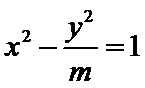
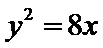
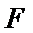
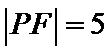
正确答案

解析

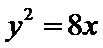
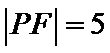
因为P在抛物线上，,

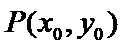
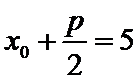
所以满足，

所以，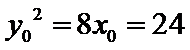

解得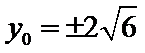,因为点P在双曲线上，

将P点坐标带入，可得m=3,

所以渐近线方程为，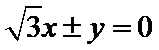

所以选C.

考查方向

双曲线的性质抛物线的性质

解题思路

以PF等于5为突破口，建立方程，求出m的值，进而求出双曲线的渐近线方程

易错点

建立方程后，解方程错误

知识点

双曲线的几何性质抛物线的标准方程和几何性质

继续学习学习下一知识点

下一知识点 : 抛物线焦点弦的性质

百度题库 > 高考 > 理科数学 > 抛物线的标准方程和几何性质

扫码查看完整答案与解析