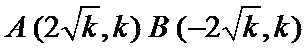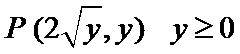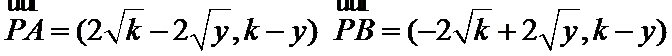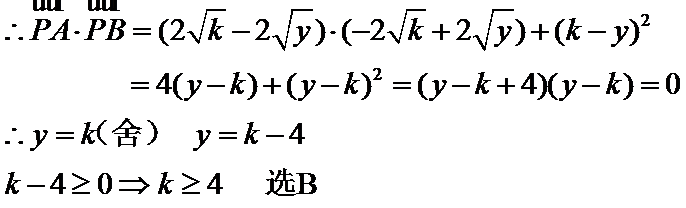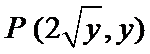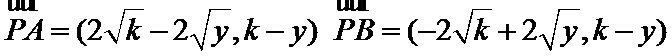抛物线的标准方程和几何性质
共238题

· 抛物线的标准方程和几何性质

抛物线的标准方程和几何性质
共238题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

15.已知抛物线上一点到焦点的距离为5，则的面积为　　　　　　．

正确答案

解析

由抛物线定义，，

所以，

所以，的面积．

应填2．

考查方向

本题主要考查抛物线的定义及抛物线的标准方程等知识，难度不大，考查数形结合思想和运算能力。

解题思路

本题主要考查抛物线的定义及抛物线的标准方程等知识，

解题步骤如下：

由抛物线定义求出P点坐标；

由三角形面积公式，求出结果。

易错点

不能根据定义正确求出P点坐标。

知识点

抛物线的定义及应用抛物线的标准方程和几何性质

题型：单选题

单选题 · 5 分

6.如果，，…，是抛物线：上的点，它们的横坐标依次为，，…，，是抛物线的焦点，若，则

正确答案

解析

由抛物线方程知p=2，结合焦半径公式|PF|=，=，故选A。

考查方向

本题主要考查了抛物线的性质及焦半径公式，在近几年的各省高考题经常出现，抛物线常与直线结合出题，即圆锥曲线与直线的位置关系。

解题思路

因为|PF|=，所以直接利用抛物线的焦半径公式就可求得。

易错点

1,由抛物线标准方程求不出P;

2、不能正确掌握抛物线的焦半径公式。

知识点

抛物线的标准方程和几何性质抛物线焦点弦的性质

题型：单选题

单选题 · 5 分

9．已知F是抛物线y2=4x的焦点，点A，B在该抛物线上且位于x轴的两侧，OA⊥OB（其中O为坐标原点），则△AOB与△AOF面积之和的最小值是（　　）

A16

D18

正确答案

解析

设直线AB的方程为：x=ty+m，

点A（x1，y1），B（x2，y2），直线AB与x轴的交点为M（m，0），

x=ty+m代入y2=4x，可得y2﹣4ty﹣4m=0，

根据韦达定理有y1•y2=﹣4m，

∵OA⊥OB， ∴•=0，

∴x1•x2+y1•y2=0，从而（y1•y2）2+y1•y2=0，

∵点A，B位于x轴的两侧，

∴y1•y2=﹣16，故m=4．

不妨令点A在x轴上方，则y1＞0，

又F（1，0），

∴S△ABO+S△AFO=×4×（y1﹣y2）+×y1=y1+≥8，

当且仅当y1=，即y1=时，取“=”号，

∴△ABO与△AFO面积之和的最小值是8，

故选：C．

考查方向

本题主要考查抛物线的定义及直线与抛物线综合应用，也在题目中考查了向量在圆锥曲线中的应用等知识，意在考查考生的运算求解能力和分析解决问题能力，在近几年的各省高考题出现的频率较高，常与向量，基本不等式等知识点交汇处命题，较难。

解题思路

1、先设直线方程和点的坐标，联立直线与抛物线的方程得到一个一元二次方程，再利用韦达定理及•=0，得到y1•y2。2、最后将面积之和表示出来，得到最值问题。

易错点

1、设直线方程时未考虑到斜率是否存在而出错。2、再把S△ABO+S△AFO转化成坐标形式时容易出错。

知识点

抛物线的标准方程和几何性质圆锥曲线中的范围、最值问题

题型：单选题

单选题 · 5 分

10.已知抛物线，直线（k为常数）与抛物线交于A,B两个不同点，若在抛物线上存在一点P(不与A,B重合)，满足，则实数k的取值范围为

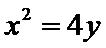
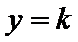
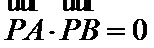
正确答案

解析

抛物线与直线y=k联立确定AB两点的坐标

设动点

则

考查方向

本题主要考察了抛物线的定义及其标准方程，考察了抛物线的几何意义，考察了向量的数量积运算，考察了向量的坐标运算，考察了存在性问题求解，该题多知识点交汇，题目较难，解题多注意细节

解题思路

本题属于多知识迁移题，需要对知识进行有效转换

（1）确定AB两点的坐标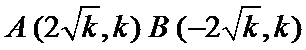以及动点

（2）向量

（3）利用向量的数量积运算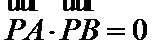得出关于y的方程，方程有正解

易错点

该题主要易错于题意理解错误，不能有效进行知识的转换

知识点

量积判断两个平面向量的垂直关系抛物线的标准方程和几何性质

题型：单选题

单选题 · 5 分

2．抛物线的准线与轴的交点的坐标为（）

正确答案

解析

抛物线的准线方程为x=-1,与轴的交点的坐标为

考查方向

本题主要考查了抛物线的几何性质，属于简单题，是高考的热点，解决此类题的关键是记住抛物线的准线方程。

易错点

本题易在记忆抛物线的准线方程出错。

知识点

抛物线的标准方程和几何性质

继续学习学习下一知识点

下一知识点 : 抛物线焦点弦的性质

百度题库 > 高考 > 理科数学 > 抛物线的标准方程和几何性质

扫码查看完整答案与解析