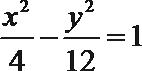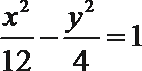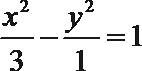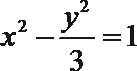- 抛物线的标准方程和几何性质
- 共238题
抛物线

正确答案
解析
根据抛物线





考查方向
本题主要考查了抛物线准线的定义与双曲线的渐近线的定义的综合应用
易错点
容易记错抛物线准线的定义
知识点
7.设双曲线

同,则此双曲线的方程为
正确答案
解析
由c=1,且焦点在y轴上,得a=2b。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
本题主要考查双曲线的标准方程
解题思路
1、求出c;
2、利用a,b,c关系求a,b,即可得到结果。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
本题易在判断焦点位置时发生错误。
知识点
13.抛物线








正确答案
解析
设抛物线

则
∵直线


∴可设直线

联立直线

消
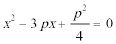
又∵
∴
∴抛物线方程为
考查方向
本题考查抛物线的简单性质,考查数形结合能力,注意解题方法的积累,属于中档题
解题思路
通过设抛物线

可得直线

联立直线方程和抛物线方程,
消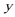
易错点
无
知识点
如图,已知抛物线




















给出下列三个结论:
① 数列
② 对任意

③ 若


所有正确结论的序号是_____.
正确答案
① ② ③
解析
由题意,知数列







考查方向
本题主要考查抛物线的性质与数列的综合应用
易错点
抛物线性质与数列的结合处
知识点
7.已知双曲线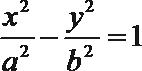
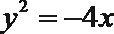
正确答案
解析
双曲线的左焦点为(-2,0),即c=2,所以a=1,b2=3,所以选D
考查方向
本题主要考查双曲线与抛物线的几何性质,属于简单题
解题思路
先求出a,b的值,进而求解问题
易错点
双曲线的标准方程等基础概念
知识点
扫码查看完整答案与解析