- 抛物线的标准方程和几何性质
- 共238题
14.已知抛物线


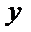



正确答案
2
解析
如图,由题意可得 AF=AC设AF=3m,由AB=2BC,可AB=2m,BC=m,过A作AD垂直x轴于D,设A的横坐标为


考查方向
解题思路
画出抛物线简图,用抛物线定义,结合题中的位置关系,数量关系,求出点A(2,2
易错点
对抛物线定义及性质掌握不熟
知识点
.
23.求抛物线
24.已知动圆







正确答案
(1)
解析
(1) 设抛物线的焦点为

由







考查方向
解题思路
联立直线与抛物线方程,求解抛物线过焦点的弦长.
设动圆圆心

易错点
联立消元计算出错
第2问计算量较大,对学生的运算能力是个严重的考验。
不能正确地两次利用基本不等式求最值。
正确答案
(2)
解析
设动圆圆心

且圆
令

解得:
设
当

当





综上①知



当且仅当

所以

考查方向
解题思路
联立直线与抛物线方程,求解抛物线过焦点的弦长.
设动圆圆心

易错点
联立消元计算出错
第2问计算量较大,对学生的运算能力是个严重的考验。
不能正确地两次利用基本不等式求最值。
已知抛物线


23.求抛物线C的方程;
24.已知动圆P的圆心在抛物线C上,且过定点D(0,4),若动圆P与x轴交于A、B两点,且

正确答案
(Ⅰ)
解析
(1) 设抛物线的焦点为

由








考查方向
解题思路
过抛物线焦点的弦长运用抛物线的定义可求得;求出
易错点
本题抛物线为开口向上的,故焦点弦长为

正确答案

解析
设动圆圆心

且圆
令

解得:

当

当




所以

考查方向
解题思路
过抛物线焦点的弦长运用抛物线的定义可求得;求出
易错点
本题抛物线为开口向上的,故焦点弦长为

动点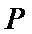
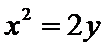
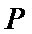

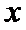
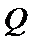
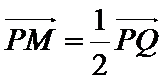
23.求点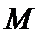
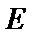
24.设点




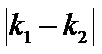
正确答案
详见解析
解析
解:(Ⅰ)设点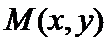
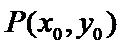
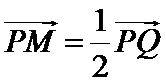
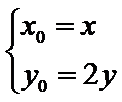
因为点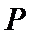

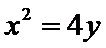
考查方向
求圆锥曲线的轨迹方程
解题思路
设参数,找等量关系,求解参数
易错点
计算能力弱,数形结合思想运用不牢
教师点评
解析几何一般都需要学生拥有一个强大的计算能力
正确答案
详见解析
解析
(Ⅱ)由已知,直线的斜率一定存在,
设点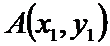
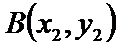
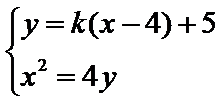
得,
由韦达定理,得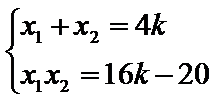
当直线经过点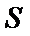
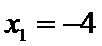

当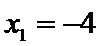
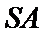
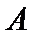
则 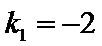

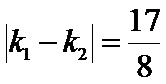
同理,当点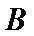
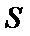

直线不经过点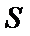
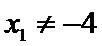

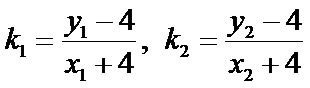


故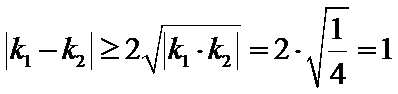
所以
考查方向
抛物线的性质及应用,直线和圆锥曲线的交汇问题 直线的斜率,求圆锥曲线的轨迹方程
解题思路
设出相关点的坐标,利用直线和圆锥曲线的方程联立,带入坐标,求解参数的值,利用平均值不等式判断求解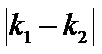
易错点
计算能力弱,不会用平均值不等式求最值
已知抛物线C的标准方程为

23.求抛物线C的标准方程;
24.记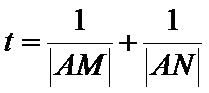
正确答案
抛物线C的标准方程为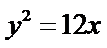
解析
由题意,

抛物线C的标准方程为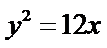
考查方向
求抛物线的标准方程,圆锥曲线和直线的交汇问题
解题思路
根据三角形的面积公式,抛物线的几何性质,建立关于p的方程,然后求出p
易错点
抛物线的几何性质掌握不好,计算求解错误
教师点评
主要是找到等量关系,建立方程,进而求出p
正确答案
不论a取何值,t均与m有关, 即
仅当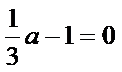

解析
设
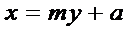
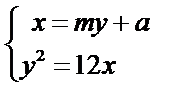

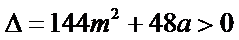
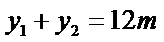


(ⅰ)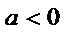


又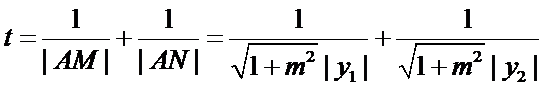
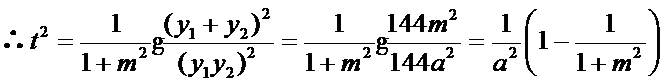
不论a取何值,t均与m有关, 即
(ⅱ)





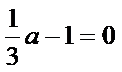

考查方向
求抛物线的标准方程,圆锥曲线和直线的交汇问题
解题思路
设出相关变量的参数,然后联立成方程组,利用代数方法解决几何问题。
在讨论a时,要对a的符号进行讨论,最后结合讨论结果,给出答案。
教师点评
本题主要难在计算量上,在设参数然后“解析”的时候,要注意运算正确
扫码查看完整答案与解析