- 抛物线的标准方程和几何性质
- 共238题
设函数f(x)=
正确答案
解析
当x>0时,f(x)=
f[f(x)]=


知识点
如图,在正方形














(1)求证:点

(2)过点







正确答案
(1)

解析
(1)依题意,过



设






(2)依题意:直线

由
此时


设:
又
分别带入
直线


知识点
若函数f(x)=x3+ax2+bx+c有极值点x1,x2,且f(x1)=x1,则关于x的方程3(f(x))2+2af(x)+b=0的不同实根个数是( )。
正确答案
解析
解析:
由f′(x)=3x2+2ax+b=0得,x=x1或x=x2,
即3(f(x))2+2af(x)+b=0的根为f(x)=x1或f(x)=x2的解,如图所示,
由图象可知f(x)=x1有2个解,f(x)=x2有1个解,因此3(f(x))2+2af(x)+b=0的不同实根个数为3.
知识点
若曲线



正确答案

解析




知识点
设a,b,c均为正数,且a+b+c=1,证明:
(1)ab+bc+ac≤
(2)
正确答案
见解析
解析
(1)由a2+b2≥2ab,b2+c2≥2bc,c2+a2≥2ca,
得a2+b2+c2≥ab+bc+ca.
由题设得(a+b+c)2=1,即a2+b2+c2+2ab+2bc+2ca=1.
所以3(ab+bc+ca)≤1,即ab+bc+ca≤
(2)因为


故
即
所以
知识点
设△ABC的内角A,B,C所对的边分别为a,b,c,若bcos C+ccos B=asin A,则△ABC的形状为( )。
正确答案
解析
∵bcos C+ccos B=asin A,由正弦定理得sin Bcos C+sin Ccos B=sin2A,∴sin(B+C)=sin2A,即sin A=sin2A。又sin A>0,∴sin A=1,∴
知识点
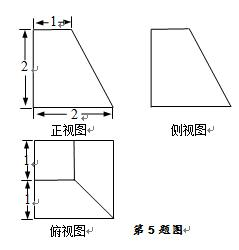
某四棱台的三视图如图1所示,则该四棱台的体积是 ( )
正确答案
解析
B;由三视图可知,该四棱台的上下底面边长分别为1和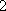
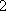
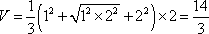
知识点
已知双曲线

正确答案
解析
设A点坐标为(x0,y0),则由题意,得S△AOB=|x0|·|y0|=








知识点
设函数f(x)=ax-(1+a2)x2,其中a>0,区间I={x|f(x)>0}。
(1)求I的长度(注:区间(α,β)的长度定义为β-α);
(2)给定常数k∈(0,1),当1-k≤a≤1+k时,求I长度的最小值。
正确答案
(1) 

解析
(1)因为方程ax-(1+a2)x2=0(a>0)有两个实根x1=0,
故f(x)>0的解集为{x|x1<x<x2}。
因此区间

(2)设d(a)=

令d′(a)=0,得a=1.
由于0<k<1,故当1-k≤a<1时,d′(a)>0,d(a)单调递增;
当1<a≤1+k时,d′(a)<0,d(a)单调递减。
所以当1-k≤a≤1+k时,d(a)的最小值必定在a=1-k或a=1+k处取得。
而
故d(1-k)<d(1+k)。
因此当a=1-k时,d(a)在区间[1-k,1+k]上取得最小值
知识点
在△ABC中,a=3,
(1)求cos A的值;
(2)求c的值。
正确答案
(1) 
解析
(1)因为a=3,
所以在△ABC中,由正弦定理得
所以

(2)由(1)知,cos A=
所以sin A=
又因为∠B=2∠A,
所以cos B=2cos2A-1=
所以sin B=
在△ABC中,sin C=sin(A+B)=sin Acos B+cos Asin B=
所以c=
知识点
扫码查看完整答案与解析