- 抛物线的标准方程和几何性质
- 共238题
抛物线


正确答案
解析
:函数






所求面积为
知识点
设







(1)求

(2)若

(3)当


正确答案
见解析
解析
(1)

(2)假设


那么可以设
其中



由



因为

而
所以

(3)由


同理

由数学归纳法知,对任意

即对任意

因此,存在


则


可得对任意


设


若



若


取


知识点
复数


正确答案
解析
略
知识点
已知函数
(1)求函数
(2)试探究函数
(3)若


正确答案
见解析。
解析
解:(1)由
① 当




② 当





综合①②的当


当



(2)函数
又
令
则
故函数


有由(1)知当

即




随着









故①当

②当

③当

(3)由(2)知当


先分析法证明:
要证
只需证
即证
构造函数
故函数


则
①当




②当



故当


综合①②得,满足题意的实数

知识点
如图7,直线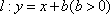
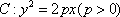
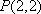
物线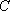
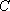
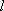

(1)求直线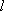
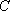
(2)过点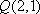
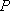
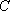
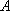

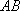
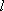
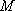
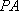
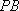
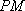
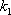
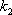
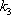
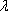
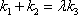
正确答案
见解析。
解析
(1)(法一)

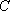
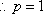
设与直线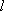
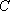
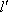
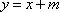
由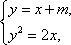
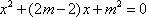
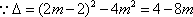

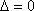
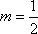
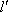
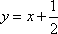

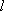


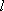

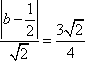

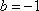


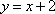

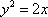
(法二)

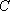
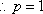


设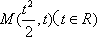
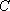
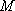
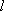

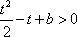
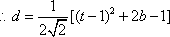
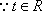
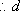
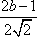
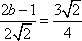
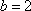
因此,直线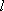
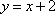
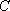
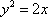
(2)
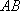

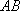
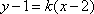

由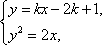
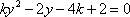
设点
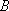
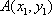
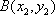
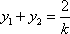

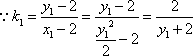

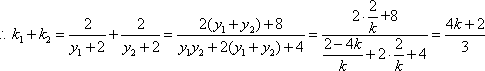
由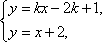
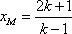
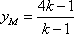
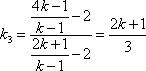
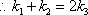
因此,存在实数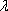
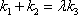
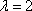
知识点
扫码查看完整答案与解析