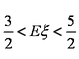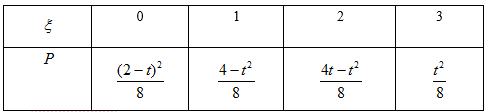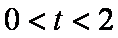- 随机事件及其概率
- 共504题
某学校对高三学生一次模拟考试的数学成绩进行分析,随机抽取了部分学生的成绩,得到如图所示的成绩频率分布直方图。
(1)根据频率分布直方图估计这次考试全校学生数学成绩的众数、中位数和平均值;
(2)若成绩不低于80分为优秀成绩,视频率为概率,从全校学生中有放回的任选3名学生,用变量ξ表示3名学生中获得优秀成绩的人数,求变量ξ的分布列及数学期望E(ξ) 。
正确答案
(1)众数:75,中位数:75,平均值为74.6
(2)E(ξ)=
解析
(1)依题意可知,
众数:75,中位数:75,

所以综合素质成绩的的平均值为74.6。
(2)由频率分布直方图知优秀率为
由题意知ξ
故其分布列为

知识点
在长为12cm的线段AB上任取一点C.现作一矩形,领边长分别等于线段AC,CB的长,则该矩形面积小于32cm2的概率为
正确答案
解析
根据程序框图可计算得

因此输出的值与
知识点
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4。
(1)从袋中随机抽取两个球,求取出的球的编号之和不大于
(2)先从袋中随机取一个球,该球的编号为


正确答案
(1)
解析
(1)从袋子中随机取两个球,其一切可能的结果组成的基本事件有1和2,1和3,1和4,2和3,2和4,3和4,共6个
从袋中随机取出的球的编号之和不大于4的事件有1和2,1和3两个
因此,所求事件的概率是
(2)先从袋中取出一个球,记下编号为



















满足条件




所以,所求的概率为
知识点
一排9个座位坐了3个三口之家,若每家人坐在一起,则不同的坐法种数为
正确答案
解析
此排列可分两步进行,先把三个家庭分别排列,每个家庭有



知识点
某市质监部门对市场上奶粉进行质量抽检,现将9个进口品牌奶粉的样品编号为1,2,3,4,…,9;6个国产品牌奶粉的样品编号为10,11,12,…,15,按进口品牌及国产品牌分层进行分层抽样,从其中抽取5个样品进行首轮检验,用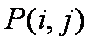
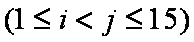
(1)求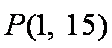
(2)求所有的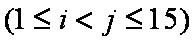
正确答案
见解析。
解析
(1)由分层抽样可知:首轮检验从编号为1,2,3,…,9的洋品牌奶粉的样品中抽取3个,从编号为10,11,…,15的国产品牌奶粉的样品中抽取2个,故
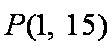
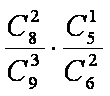
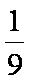
(2)①当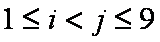
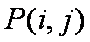
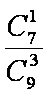
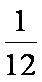
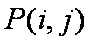
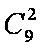
②当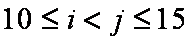
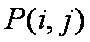
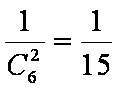
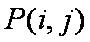
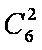
③当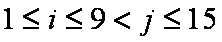
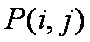
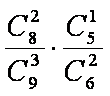
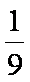
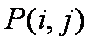
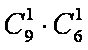
所以,所有的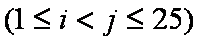
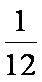
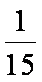
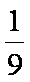
知识点
某学校为了增强学生对消防安全知识的了解,举行了一次消防安全知识竞赛,其中 一道题是连线题,要求将4种不同的工具与它们的4种不同的用途一对一连线,规定:每连对一条得5分,连错一条得-2分。某参赛者随机用4条线把消防工具与用 途一对一全部连接起来。
(1)求该参赛者恰好连对一条的概率。
(2)设X为该参赛者此题的得分,求X的分布列与数学期望。
正确答案
(1)
解析
(1)
(2) 









且
知识点
现有甲、乙、丙三人参加某电视台的应聘节目非你莫属,若甲应聘成功的概率为 ,乙、丙应聘成功的概率均为(0<t<2),且三个人是否应聘成功是相互独立的。
(1)若乙、丙有且只有一个人应聘成功的概率等于甲应聘成功是相互独立的,求t的值;
(2)记应聘成功的人数为ξ,若当且仅当ξ为2时概率最大,求E(ξ)的取值范围。
正确答案
(1)t=1(2)
解析
解析:(1)由题意得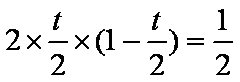
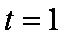
(2)
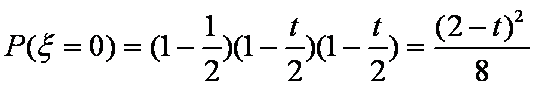
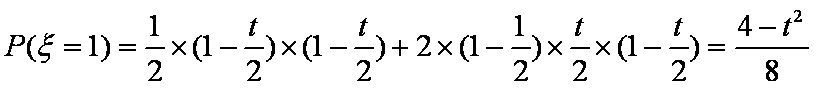
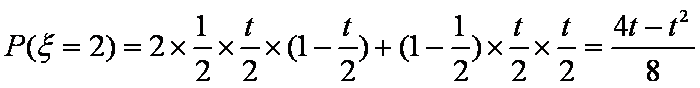
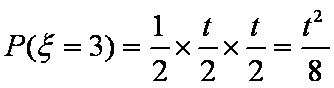
故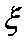
……………………7分
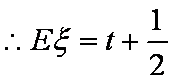
由题意得: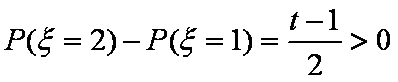

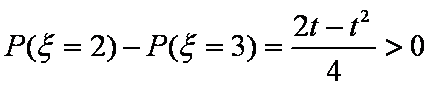
所以解得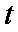
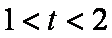
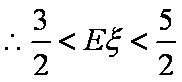
知识点
2013年12月21日上午10时,省会首次启动重污染天气Ⅱ级应急响应,正式实施机动车车尾号限行,当天某报社为了解公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
(1)完成被调查人员的频率分布直方图;
(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行进行追踪调查,记选中的4人中不赞成“车辆限行”的人数为ξ,求随机变量ξ的分布列和数学期望。
正确答案
见解析
解析
(1)各组的频率分别是
所以图中各组的纵坐标分别是
……………………5分
(2)

所以
……11分
所以

知识点
某校举行中学生“珍爱地球·保护家园”的环保知识比赛,比赛分为初赛和复赛两部分,初赛采用选手从备选题中选一题答一题的方式进行;每位选手最多有5次答题机会,选手累计答对3题或答错3题即终止比赛,答对3题者直接进入复赛,答错3题

(1)求选手甲进入复赛的概率;
(2)设选手甲在初赛中答题的个数为,试求的分布列和数学期望。
正确答案
见解析
解析
(1)设“选手甲进入复赛”为事件,则选手甲答了3题都对进入复赛概率为:
或选手甲答了4个题,前3个2对1错,第4次对进入复赛

选手甲进入复赛的概率
(2)的可能取值为3,4,5,对应的每个取值,选手甲被淘汰或进入复赛的概率

的分布列为:

知识点
某商场为了了解顾客的购物信息,随机的在商场收集了100位顾客购物的相关数据,整理如下:
统计结果显示:100位顾客中购物款不低于100元的顾客占60%。据统计该商场每日大约有5000名顾客,为了增加商场销售额度,对一次性购物不低于100元的顾客发放纪念品(每人一件).(注:视频率为概率)
(1)试确定m,n的值,并估计该商场每日应准备纪念品的数量;
(2)现有4人去该商场购物,求获得纪念品的人数ξ的分布列与数学期望.
正确答案
见解析
解析
解析:(1)由已知,100位顾客中购物款不低于100元的顾客有


该商场每日应准备纪念品的数量大约为 
(2)由(1)可知1人购物获得纪念品的频率即为概率

故4人购物获得纪念品的人数



……………………11分

或由
知识点
扫码查看完整答案与解析