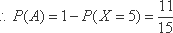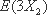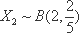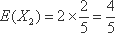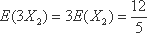- 古典概型与几何概型
- 共235题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
从0,1,2,3,4,5,6,7,8,9中任取七个不同的数,则这七个数的中位数是6的概率为 。
正确答案
解析
6之前6个数中取3个,6之后3个数中取3个,
知识点
随机抽取9个同学中,至少有2个同学在同一月出生的概率是 (默认每月天数相同,结果精确到
正确答案
0.985
解析
9位同学生日月份的可能有

故至少有2个同学在同一月出生的概率为

知识点
将一枚均匀的硬币投掷6次,则正面出现的次数比反面出现的次数多的概率为
正确答案
解析
硬币投掷6次,有三类情况,①正面次数比反面次数多;②反面次数比正面次数多;③正面次数而后反面次数一样多;,③概率为
知识点
从个位数与十位数之和为奇数的两位数中任取一个,其中个位数为
正确答案
解析
首先求“个位数与十位数之和为奇数的两位数”的个数,利用“奇数+偶数=奇数”分两种情况求:①即十位数字分别为1,3,5,7,9时,个位数字可以为:0,2,4,6,8,此时有





知识点
有甲、乙两个篮球运动员,每人各投篮三次,甲三次投篮命中率均为

如果又未中,则乙进行第三次投篮,并且在投篮时距离为16米,乙若投中,则不再继续
投篮,且知乙命中的概率与距离的平方成反比。
(1)求乙投篮命中的概率;
(2)求甲三次投篮命中次数ξ的期望与方差,
正确答案
见解析。
解析
(1)记乙三次投篮依次为事件A、B、C,设乙命中概率与距离的平方成反比的比例系
数为a,则由题意得:

故乙投篮命中的概率为

(2)甲重复三次投篮的命中次数ξ服从二项分布,即
则
知识点
设


(1)记使得“

(2)设


正确答案
见解析。
解析
(1)由


由于整数


(2)由于



且有



故
所以

知识点
在一场娱乐晚会上,有5位民间歌手(1至5号)登台演唱,由现场数百名观众投票选出最受欢迎歌手,各位观众须彼此独立地在选票上选3名歌手,其中观众甲是1号歌手的歌迷,他必选1号,不选2号,另在3至5号中随机选2名,观众乙和丙对5位歌手的演唱没有偏爱,因此在1至5号中随机选3名歌手。
(1)求观众甲选中3号歌手且观众乙未选中3号歌手的概率;
(2)X表示3号歌手得到观众甲、乙、丙的票数之和,求X的分布列及数学期望。
正确答案
(1) 
解析
(1)设A表示事件“观众甲选中3号歌手”,B表示事件“观众乙选中3号歌手”,
则P(A)=

∵事件A与B相互独立,
∴观众甲选中3号歌手且观众乙未选中3号歌手的概率为P(A


(2)设C表示事件“观众丙选中3号歌手”,则P(C)=
∵X可能的取值为0,1,2,3,且取这些值的概率分别为
P(X=0)=
P(X=1)=
=
P(X=2)=P(AB



P(X=3)=P(ABC)=
∴X的分布列为
∴X的数学期望
知识点
某联欢晚会举行抽奖活动,举办方设置了甲,乙两种抽奖方案,方案甲的中奖率为

(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为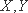

(2)若小明,小红两人都选择方案甲或方案乙进行抽奖,问:他们选择何种方案抽奖,累计的得分的数学期望较大?
正确答案
见解析
解析
(1)由已知得:小明中奖的概率为

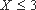
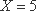
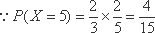

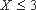
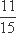
(2)设小明,小红都选择方案甲抽奖中奖的次数为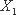
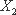
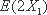
由已知: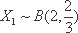
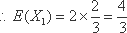
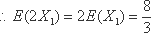

知识点
扫码查看完整答案与解析