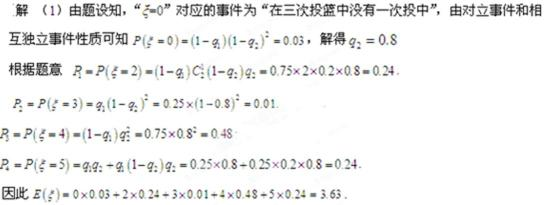- 随机事件及其概率
- 共504题
18.某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:


(1)求图中实数
(2)若该校高一年级共有学生640人,试估计该校高一年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在

正确答案
(1)由于图中所有小矩形的面积之和等于1,
所以
解得
(2)根据频率分布直方图,成绩不低于60分的频率为
由于该校高一年级共有学生640人,利用样本估计总体的思想,可估计该校高一年级数学成绩不低于60分的人数约为
(3)成绩在



成绩在





若从数学成绩在
















如果两名学生的数学成绩都在



记“这两名学生的数学成绩之差的绝对值不大于10”为事件








所以所求概率为
解析
解析已在路上飞奔,马上就到!
知识点
17.某学校要用三辆校车从老校区把教职工接到校本部,已知从老校区到校本部有两条公路,校车走公路①堵车的概率为



(1)若三辆校车中恰有一辆校车被堵的概率为
(2)在(1)的条件下,求三辆校车中被堵车辆的辆数
正确答案
解:(1)由已知条件得
即

答:的值为
(2)解:



所以
答:数学期望为
解析
解析已在路上飞奔,马上就到!
知识点
19.A、B是治疗同一种疾病的两种药,用若干试验进行对比试验,每个试验由4只小白鼠组成,其中2只服用A,另两只服用B,然后观察疗效,若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组,设每只小白鼠服用A有效的概率为

(1)求一个试验组为甲类组的概率;
(2)观察3个试验组,用

正确答案
解:(Ⅰ)设A1表示事件“一个试验组中,服用A有效的小白鼠有i只”,i= 0,1,2,
B1表示事件“一个试验组中,服用B有效的小白鼠有i只”,i= 0,1,2,依题意有
所求的概率为P = P(B0·A1)+ P(B0·A2)+ P(B1·A2=
(Ⅱ)ξ的可能值为0,1,2,3且ξ~B(3,
ξ的分布列为
数学期望
解析
解析已在路上飞奔,马上就到!
知识点
20.在某学校组织的一次篮球定点投篮训练中,规定每人最多投3次:在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次。某同学在A处的命中率q1为0.25,在B处的命中率为q2,该同学选择先在A处投一球,以后都在B处投,用ξ表示该同学投篮训练结束后所得的总分,其分布列为
(1)求随机变量ξ的数学期望E(ξ);
(2)试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。
正确答案
(2)用C表示事件“该同学选择第一次在A处投,以后都在B处投,得分超过3分”,
用D表示事件“该同学选择都在B处投,得分超过3分”,
则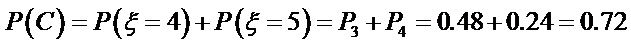
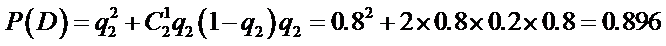
故P(D)>P(C).
即该同学选择都在B处投篮得分超过3分的概率大于该同学选择第一次在A处投以后都在B处投得分超过3分的概率。
解析
解析已在路上飞奔,马上就到!
知识点
5 .五名同学报考五所名牌大学的自主招生.已知考试分笔试与面试,每人笔试通过的概率都是

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.甲、乙、丙三人组成一组,参加一个闯关游戏团体赛,三人各自独立闯关,其中甲闯关成功的概率为


(1)求乙、丙各自闯关成功的概率;
(2)求团体总分为4分的概率;
(3)若团体总分不小于4分,则小组可参加复赛,求该小组参加复赛的概率.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 已知数字发生器每次等可能地输出数字

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.甲、乙、丙三名射击运动员射中目标的概率分别为

(1)求
(2)在概率


正确答案
解:(1)设




所以


(2)由


可得


即实数

解析
解析已在路上飞奔,马上就到!
知识点
18.在一次数学考试中,第22题和第23题为选做题. 规定每位考生必须且只须在其中选做一题. 设某4名考生选做每一道题的概率

(1)求其中甲、乙两名学生选做同一道题的概率;
(2)设这4名考生中选做第22题的学生个数为

正确答案
解:(1)
(2)随机变量

∴
∴变量
解析
解析已在路上飞奔,马上就到!
知识点
18.某汽车驾驭学校在学员结业前对其驾驶技术进行4次考核,规定:按顺序考核,一旦考核合格就不必参加以后的考核,否则还需参加下次考核,若小张参加每次考核合格的概率依次组成一个公差为

(1)求小张第一次参加考核就会合格的概率
(2)求小张参加考核的次数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析