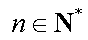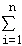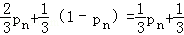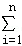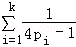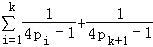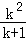- 随机事件及其概率
- 共504题
某单位为绿化环境,移栽了甲、乙两种大树各




(1)求
(2)求甲种大树成活的株数大于乙种大树成活的株数的概率;
(3)用



正确答案
见解析。
解析
设“甲种大树恰有


设“乙种大树恰有


(1)两种大树各成活

(2)设“甲种大树成活的株数大于乙种大树成活的株数”为事件
则
所以,甲种大树成活的株数大于乙种大树成活的株数的概率为
(3)由题意知,

所以


知识点
中国航母“辽宁舰”是中国第一艘航母,“辽宁”号以4台蒸汽轮机为动力,为保证航母的动力安全性,科学家对蒸汽轮机进行了170余项技术改进,增加了某项新技术,该项新技术要进入试用阶段前必须对其中的三项不同指标甲、乙、丙进行通过量化检测,假如该项新技术的指标甲、乙、丙独立通过检测合格的概率分别为


(1)求该项技术量化得分不低于8分的概率;
(2)记该项新技术的三个指标中被检测合格的指标个数为随机变量X,求X的分布列与数学期望。
正确答案
见解析。
解析
(1)该项新技术的三项不同指标甲、乙、丙独立通过检测合格分别为事件


则事件“得分不低于8分”表示为

























(2)该项新技术的三个指标中被检测合格的指标个数




























随机变量






知识点
一批产品共100件,其中有3件不合格品,从中随机抽取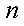
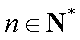
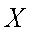
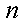
(1)若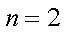
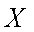
(2)求使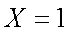
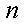
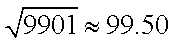
正确答案
见解析。
解析
(1)当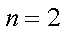
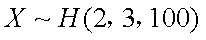
则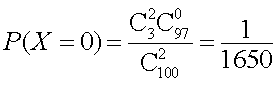
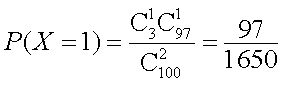
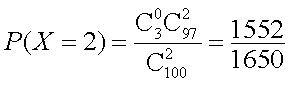
所以,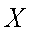
(2)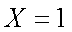
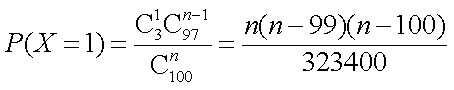
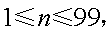
记函数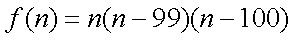
则由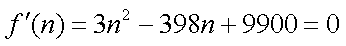
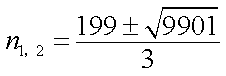
由参考数据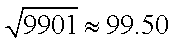
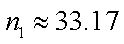
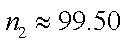
而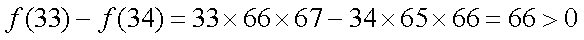
结合函数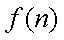
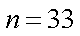
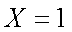
知识点
从棱长为1的正方体的8个顶点中任取不同2点,设随机变量ξ是这两点间的距离。
(1)求概率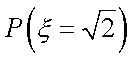
(2)求ξ的分布列,并求其数学期望E(ξ)。
正确答案
见解析。
解析
(1)从正方体的8个顶点中任取不同2点,共有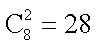
因为正方体的棱长为1,所以其面对角线长为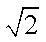
正方体每个面上均有两条对角线,所以共有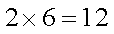
因此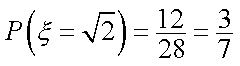
(2)随机变量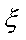
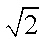
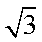
正方体的棱长为1,而正方体共有12条棱,于是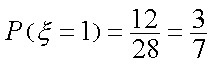
从而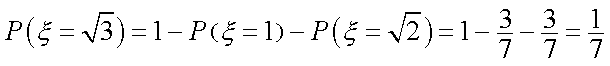
所以随机变量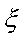
因此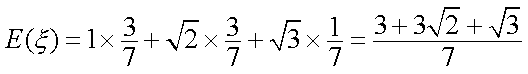
知识点
2013年2月20日,针对房价过高,国务院常务会议确定五条措施(简称“国五条”),为此,记者对某城市的工薪阶层关于“国五条”态度进行了调查,随机抽取了60人,作出了他们的月收入的频率分布直方图(如图),同时得到了他们的月收入情况与“国五条”赞成人数统计表(如下表):
(1)试根据频率分布直方图估计这60人的平均月收入;
(2)若从月收入(单位:百元)在[15,25),[25,35)的被调查者中各随机选取3人进行追踪调查,记选中的6人中不赞成“国五条”的人数为X,求随机变量X的分布列及数学期望。
正确答案
见解析
解析
解析:(1)这

(2)根据频率分布直方图可知







∴
∴
知识点
在一个盒子中有分别标有数字1,2,3,4,5的5张卡片,现从中一次取出2张卡片,则取到的卡片上的数字之积为偶数的概率是 。
正确答案
解析
从标有数字1,2,3,4,5的5张卡片中一次取出2张卡片,共有
其中取到的卡片上的数字之积为偶数分为两种情况:一类是取得的两个数字都是偶数:只有一种情况(2,4);
另一类是一个偶数和一个奇数,有
∴取到的卡片上的数字之积为偶数的概率P=
知识点
已知矩阵M=
(1)求实数a,b的值;
(2)求曲线C′的方程。
正确答案
(1)∴
(2)
解析
(1)由已知得M



∴
(2)设点P(x',y')是曲线C:xy=1上的任意一点,变换后的点为P'(x,y)
则



因为x′y′=1,所以

知识点
我省某示范性高中为推进新课程改革,满足不同层次学生的要求,决定从高一年级开始,在每周的周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座,每位有兴趣的同学可以在期间的任何一天参加任何一门科目的辅导讲座,也可以放弃任何一门科目的辅导讲座(规定:各科达到预先设定的人数时称为满座,否则称为不满座),统计数据表明,各学科讲座各天的满座概率如下表:
(1)求数学辅导讲座在周一、周三、周五都不满座的概率;
(2)设周三各辅导讲座满座的科目数为

正确答案
见解析
解析
解析:(1)设数学辅导讲座在周一、周三、周五都不满座为事件

(2)







所以,随机变量

故
知识点
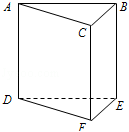
如图,一颗棋子从三棱柱的一个顶点沿棱移到相邻的另一个顶点的概率均为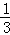
(1)求p1,p2的值;
(2)求证: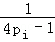
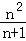
正确答案
见解析
解析
(1)棋子在上底面点A处,若移了n次后,棋子落在上底面顶点,棋子从A出发,由3条路径,所以p1=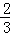
棋子移动两次,还在上底面时,有两种可能,p2=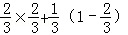
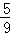
(2)因为移了n次后,棋子落在上底面顶点的概率为pn。
故落在下底面顶点的概率为1﹣pn。
于是,移了n+1次后,棋子落在上底面顶点的概率记为pn+1=
,从而pn+1﹣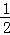
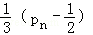
所以数列{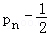
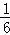
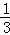
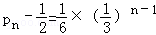
用数学归纳法证明: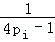
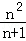
①当n=1时左式=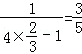
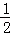
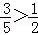
当n=2时,左式=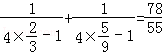
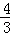
②假设n=k(k≥2)不等式成立,即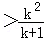
则n=k+1时,左式=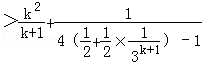
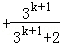
要证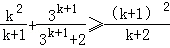
只要证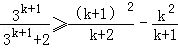
即证: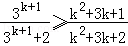
只要证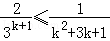
只要证3k+1≥2k2+6k+2,
因为k≥2,所以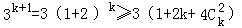
所以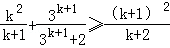
即n=k+1时不等式也成立,由①②可知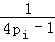
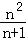
知识点
如图,设







正确答案
解析
将








知识点
扫码查看完整答案与解析