- 幂函数的图像
- 共175题
已知
(1)求函数
(2)在




正确答案
见解析。
解析
(1)因为

=

所以函数


(2)因为





在

从而S△ABC=
知识点
已知数列

(1)证明:数列

(2)设

正确答案
见解析。
解析
(1)由
当

即
∴

又

∴
(2)
∴
=
知识点
已知极坐标系的极点在直角坐标系的原点处,极轴与x轴的正半轴重合,直线l的参数方程为:
(1)写出C的直角坐标方程,并指出C是什么曲线;
(2)设直线l与曲线C相交于P、Q两点,求|PQ|值。
正确答案
(1)半径为2的圆(2)
解析
(1)∵ρ=4cosθ,∴ρ2=4ρcosθ,(2分)
由ρ2=x2+y2,ρcosθ=x得:x2+y2=4x,
所以曲线C的直角坐标方程为(x﹣2)2+y2=4,…(4分)
它是以(2,0)为圆心,半径为2的圆,…(5分)
(2)把

设其两根分别为t1、t2,则
∴
知识点
(1)若


(2)若

正确答案
见解析。
解析
(1)


所以
(2)由(1)知
则由



知识点
某学校制定学校发展规划时,对现有教师进行年龄状况和接受教育程度(学历)的调查,其结果(人数分布)如表:
(1)用分层抽样的方法在35至50岁年龄段的教师中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2人,求至少有l人的学历为研究生的概率;
(2)在该校教师中按年龄状况用分层抽样的方法抽取N个人,其中35岁以下48人,50岁以上10人,再从这N个人中随机抽取l人,此人的年龄为50岁以上的概率为
正确答案
见解析
解析
(1)由题意得:抽到35岁至50岁本科生3人,研究生2人……………2分
设本科生为
从中任取2人的所有基本事件共10个:
其中至少有一人的学历为研究生的基本事件有七个:
所以至少有一人为研究生的概率为:
(2)由题意得:
35至50岁中抽取的人数为
所以

知识点
记






正确答案
答案: 3
解析
略
知识点
如图,己知直线l与抛物线
(1)若动点M满足
(2)若过点B的直线
正确答案
见解析
解析
(1)由


故的方程为
设

由
整理,得
(2)如图,由题意知直线的斜率存在且不为零,设方程为y=k(x-2)(k≠0)①
将①代入

由

则
令
由②知




知识点
已知函数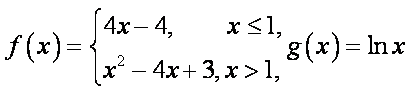
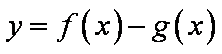
正确答案
3
解析
略
知识点
为了解某班学生喜爱打篮球是否与性别有关,对本班48人进行了问卷调查得到了如下的2×2列联表:
已知在全班48人中随机抽取1人,抽到喜爱打篮球的学生的概率为
(1)请将上面的2×2列联表补充完整(不用写计算过程);
(2)你是否有95%的把握认为喜爱打篮球与性别有关?说明你的理由。
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为X,求X的分布列与期望。
下面的临界值表供参考:
正确答案
见解析。
解析
(1)列联表补充如下:
(2)由
因为4.286>3.841,有99.5%的把握认为喜爱打篮球与性别有关.
(3)喜爱打篮球的女生人数

其概率分别为


故X的分布列为:
X的期望值为:EX=
知识点
已知
正确答案
解析
解析:



知识点
扫码查看完整答案与解析

































