- 幂函数的图像
- 共175题
1
题型:简答题
|
已知极坐标系的极点在直角坐标系的原点处,极轴与x轴的正半轴重合,直线l的参数方程为:
(1)写出C的直角坐标方程,并指出C是什么曲线;
(2)设直线l与曲线C相交于P、Q两点,求|PQ|值。
正确答案
(1)半径为2的圆(2)
解析
(1)∵ρ=4cosθ,∴ρ2=4ρcosθ,(2分)
由ρ2=x2+y2,ρcosθ=x得:x2+y2=4x,
所以曲线C的直角坐标方程为(x﹣2)2+y2=4,…(4分)
它是以(2,0)为圆心,半径为2的圆,…(5分)
(2)把

设其两根分别为t1、t2,则
∴
知识点
幂函数的图像
1
题型:填空题
|
记






正确答案
答案: 3
解析
略
知识点
幂函数的图像
1
题型:简答题
|
如图,己知直线l与抛物线
(1)若动点M满足
(2)若过点B的直线
正确答案
见解析
解析
(1)由


故的方程为
设

由
整理,得
(2)如图,由题意知直线的斜率存在且不为零,设方程为y=k(x-2)(k≠0)①
将①代入

由

则
令
由②知




知识点
幂函数的图像
1
题型:填空题
|
已知函数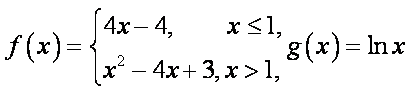
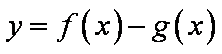
正确答案
3
解析
略
知识点
幂函数的图像
1
题型:填空题
|
已知
正确答案
解析
解析:



知识点
幂函数的图像
下一知识点 : 幂函数图象及其与指数的关系
扫码查看完整答案与解析









