- 幂函数的图像
- 共175题
已知函数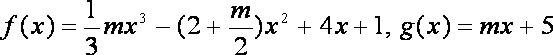
(1)当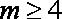

(2)是否存在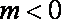
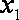


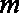
正确答案
见解析
解析
解析:(1)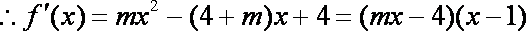
i)若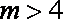
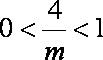

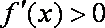
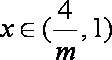
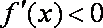
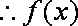
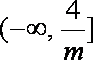
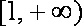
ii)若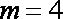
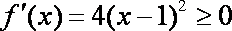
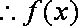
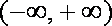
(2)当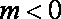
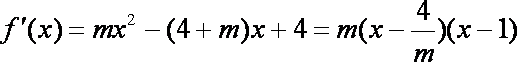
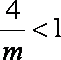
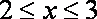

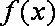
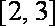
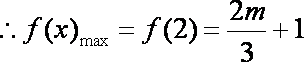
又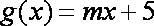
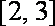
由已知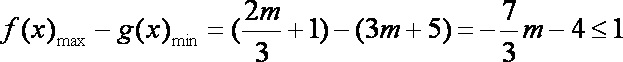
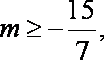

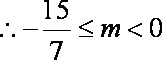
综上所述,存在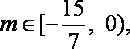
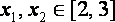
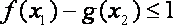
知识点
已知实数


正确答案
解析
略
知识点
已知



(1)求直线

(2)直线



正确答案
见解析
解析
解析:(1)由


所以,


设

∴

∴A(


直线

(2)连结
由椭圆的对称性可知,
所以
又由


知识点
A、B、C三点在同一球面上,

则此球O的体积为
正确答案
解析
略
知识点
已知数列



(1)求数列
(2)数列



正确答案
(1)

解析
(1)



经检验
综上 
(2)由(1)可知
=
=
=
知识点
扫码查看完整答案与解析