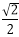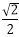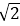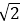对数函数的图像与性质
共44题

· 对数函数的图像与性质

对数函数的图像与性质
共44题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

4.当时,函数与函数的图象的交点个数（　　）

A可能是0个、1个或2个

B只可能是2个

C只可能是0个

D可能是3个

正确答案

解析

假定与y=x相切于(x0,y0),

则切线方程为

因为过原点,得

而

所以,

从而

那么

(1) 当时, 与y=x没有交点,

故函数与函数的图象的交点个数为零;

(2) 当时, 与y=x相切,

故函数与函数的图象的交点个数为1;

(3) 当时,y=ax与y=x有2个交点,

故函数与函数的图象的交点个数为2.

于是,正确的答案为A.

知识点

指数函数的图像与性质对数函数的图像与性质指数函数与对数函数的关系

题型：单选题

单选题 · 5 分

5.函数f(x)= 的零点个数为（　　　）

正确答案

解析

当x≤0时,

令=0⇒x=-1或x=-2;

当x>0时,令

4-x+ln x=0⇒ln x=x-4,

通过图象可知有两个交点,此时也有两个根.

所以已知函数有4个零点.

知识点

二次函数的图象和性质对数函数的图像与性质函数零点的判断和求解

题型：填空题

填空题 · 5 分

10.已知函数f(x)=loga(1+x)在区间[1,+∞)上恒有|f(x)|>2,则a的取值范围为　　　　.

正确答案

解析

若a>1,由于在区间[1,+∞)上,

得loga(1+x)>0,

因此，恒成立,

即loga(1+x)>2,得恒成立,

因为2≤x+1,那么a2<2,

结合a>1,得

若0<a<1,由于1+x>1,

得loga(1+x)<0,

因此,|f(x)|>2恒成立,

即

得a-2<x+1恒成立,

因为2≤x+1,那么a-2<2,

结合0<a<1,得<a<1.

综上得,a的取值范围为

知识点

函数恒成立问题对数函数的图像与性质对数函数的单调性与特殊点

题型：单选题

单选题 · 5 分

3.当0<x≤时,4x<logax,则a的取值范围是(　　).

A(0,)

B(,1)

C(1,)

D(,2)

正确答案

解析

∵0<x≤,∴1<4x≤2,∴logax>4x>1,

∴0<a<1,排除答案C,D;

取a=,x=,则有=2, =1,

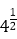
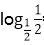
显然4x<logax不成立,排除答案A;故选B

知识点

指数函数的图像与性质对数函数的图像与性质

题型：填空题

填空题 · 5 分

15.若不等式logax>sin 2x (a>0,a≠1)对任意x∈(0,)都成立,则a的取值范围为______.

正确答案

（，1）

解析

记y1=logax,y2=sin 2x,原不等式相当于y1>y2,作出两个函数的图象,如图所示,可知当y1=logax过点A(,1)时,a=,所以当<a<1时,对任意x∈(0,)都有y1>y2.

知识点

对数函数的图像与性质正弦函数的图象不等式恒成立问题

继续学习学习下一知识点

下一知识点 : 对数函数的单调性与特殊点

百度题库 > 高考 > 理科数学 > 对数函数的图像与性质

扫码查看完整答案与解析