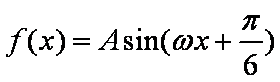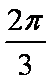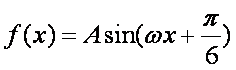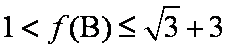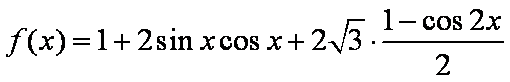- 圆系方程
- 共77题
已知







正确答案
解析
第一步识别条件:椭圆





第二步转化条件: 应该想到在向量一章里面学过这个重心的坐标表示可以用三个顶点表示啊 G((x1+x2+x3)/3,(y1+y2+y3)/3),再看看图形,发现太好了, 三个点中,F1,F2关于原点是对称的,x1+x2=0,y1+y2=0这下可好了。
第三步看问定向: 重心
第四步结论已出现:
知识点
如图,由曲线


正确答案
解析
由定积分的几何意义,阴影部分的面积等于
知识点
函数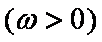
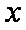
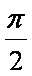
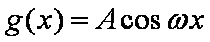
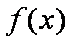
正确答案
解析
由函数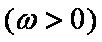
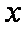
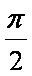
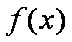
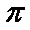
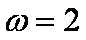
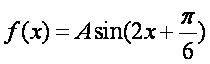
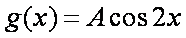
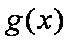
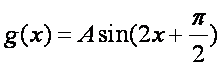
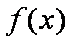
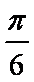
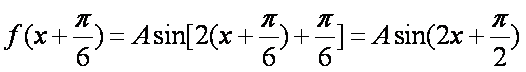
知识点
如图所示,在



(1)求点M的轨迹方程;
(2)过点




正确答案
(1)
解析
(1)设




∴


(2)设



直线



由

则
同理可得:


∴
知识点
椭圆

(1)若
(2)设直线AD,CB的斜率分别为

正确答案
见解析
解析
(1)设
由已知
又
所以
所以
符合题意,
所以,所求直线l的方程为
(2)
所以
平方得

计算得
所以
因为
所以k=3…………13分
知识点
已知函数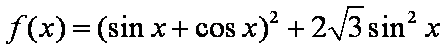
(1)求函数f (x)的最小正周期;
(2)在△ABC中,角A,B,C的对边分别是a,b,c,且满足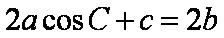
正确答案
(1)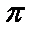
(2)
解析
(1)由已知得,
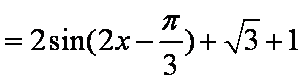
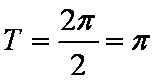
(2)由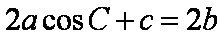
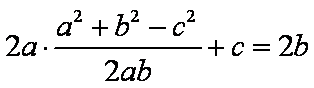
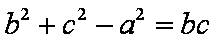
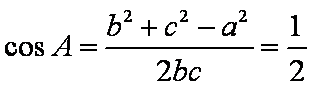
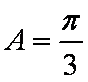
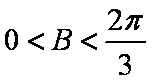
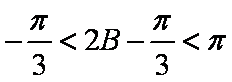
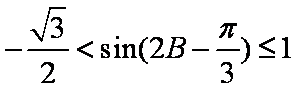
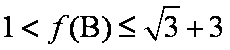
知识点
已知椭圆




(1)求椭圆
(2)设




正确答案
见解析
解析
(1): 由已知

所以
又由过焦点且垂直于长轴的直线被椭圆截得的弦长为
所以
所以
(2)设
设
整理得
得


由点

又由
所以
所以

所以


知识点
已知函数
(1)设

(2)在




正确答案
(1)

解析
(1)

由

因为
于是


(2)因为
又因

由余弦定理得
所以
由正弦定理得
所以
知识点
一个几何体的三视图如图所示,则这个几何体的体积为
正确答案
解析
略
知识点
已知椭圆
(1)当p+q
(2)若D(b+1,0),在(1)的条件下,当椭圆的离心率最小时,

正确答案
(1)
解析
(1)设半焦距为


于是圆心坐标为

整理得
即
所以


所以

(2)当


设

所以
当



当


解得
综上所述,椭圆的方程为
知识点
扫码查看完整答案与解析