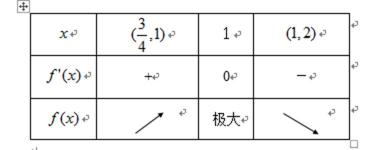
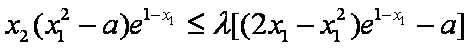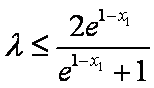- 函数单调性的性质
- 共479题
如图,三棱锥



正确答案
解析










知识点
若函数
正确答案
解析
因为函数




知识点
设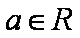
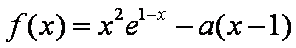
(1)当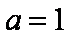
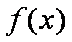
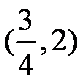
(2)设函数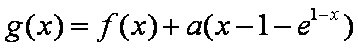
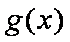
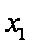
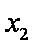
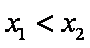
时,总有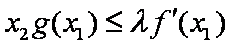
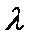
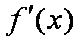
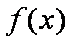
正确答案
见解析
解析
(1)当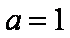
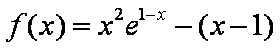
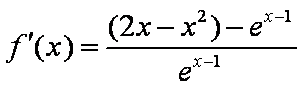
令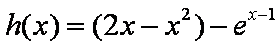
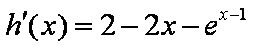
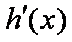
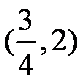
调递减.
又因为
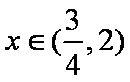
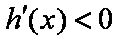
所以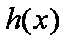
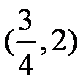
又因为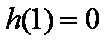
所以当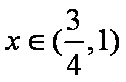
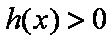
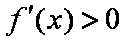
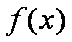
当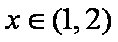
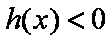
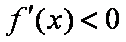
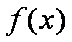
当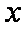
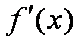
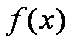
所以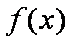
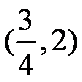
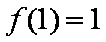
(2)由题可知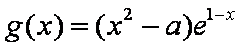
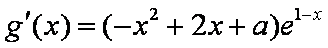
根据题意方程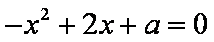
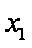
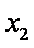
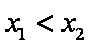
所以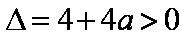
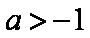
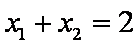
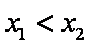
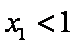
由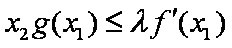
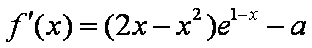
可得
又因为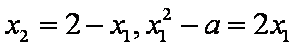
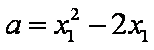
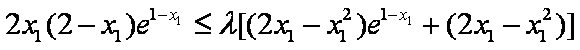
即不等式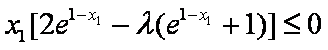
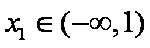
① 当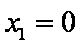
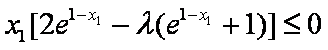
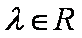
② 当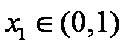
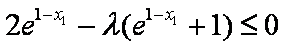
令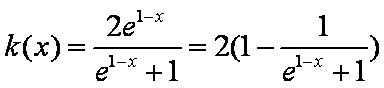
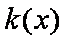
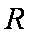
所以当
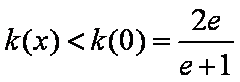
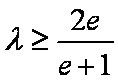
(3)当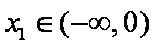
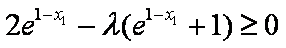
由(2)可知,当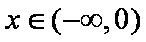
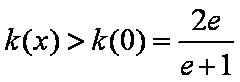
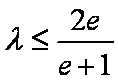
综上所述,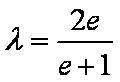
知识点
在
(1)求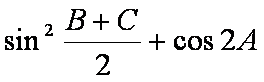
(2)若
正确答案
见解析
解析
(1)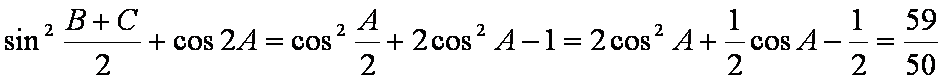
(2)
又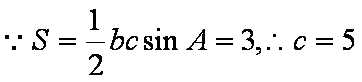
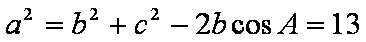
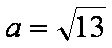
知识点
已知

(1)求
(2)若



正确答案
(1)
解析
解析:(1)函数

令

①当



所以


②当


故

③当



所以


综上,当



当



当


(2)由(1)可知
① 当


但

② 当










知识点
已知椭圆


(1)求椭圆
(2)设








(3)在 (2)的条件下,过点



正确答案
见解析
解析
解析:(1)由题意知
而以原点为圆心,椭圆短半轴为半径的圆的方程为
故由题意可知
故椭圆C的方程为
(2)由题意知直线

由
设点

直线

令
将
得
由①得
代入②整得,得
所以直线AE与x轴相交于定点Q(1,0) ……7分
(3)①当过点


解得

② 当过点

设直线



由

计算得,
所以
则
因为


所以

知识点
已知函数
(1)若关于



(2)若


正确答案
见解析
解析
(1)因为




(2)若




知识点
在极坐标系中,已知直线l的极坐标方程为


(1)求圆C的极坐标方程;
(2)求直线l被圆C所截得的弦长。
正确答案
见解析
解析
解析:(1)圆

(2)圆心到直线距离为


知识点
以下正确命题的个数为( )
①命题“存在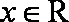
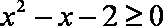
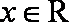
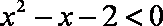
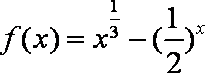
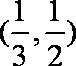
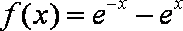
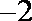
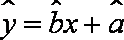
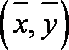
正确答案
解析
①命题的否定为“任意的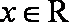
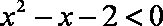
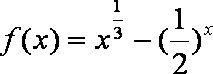
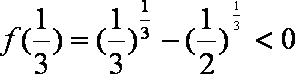
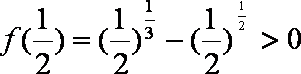
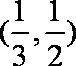
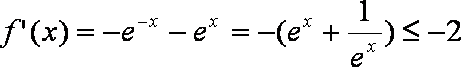
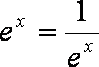
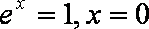
知识点
已知

(1)求

(2)若对于任意

正确答案
见解析。
解析
(1)
由



(2)



易知:
知识点
扫码查看完整答案与解析