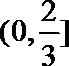- 函数单调性的性质
- 共479题
12.已知





正确答案
解析
令
由系数和


从而


易知
知识点
19.已知函数
(1)求
(2)设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数

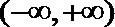

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.为了调制一种饮料,在每10kg半成品饮料中加入柠檬汁进行试验,加入量为500g到1500g之间,现用0.618法选取试点找到最优加入量,则第二个试点应选取在____________g。
正确答案
882
解析
解析已在路上飞奔,马上就到!
知识点
17. 某车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人,现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取3名工人进行技术考核.
(1)求从甲、乙两组各抽取的人数;
(2)记

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知:函数



(1)求:
(2)判断
(3)如果




正确答案
(1)解:令

(2)证明:令

令




(3)∵

∴

∵
∴(1)等价于不等式组:

则

∴
解析
解析已在路上飞奔,马上就到!
知识点
11.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析