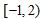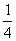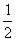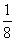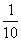- 函数单调性的性质
- 共479题
1
题型：填空题
|
已知函数f（x）=4|a|x﹣2a+1.若命题：“∃x0∈（0，1），使f（x0）=0”是真命题，则实数a的取值范围为 。
正确答案
解析
：由：“∃x0∈（0，1），使f（x0）=0”是真命题，得：
f（0）•f（1）＜0⇒（1﹣2a）（4|a|﹣2a+1）＜0
⇒
故答案为：
知识点
函数单调性的性质
1
题型：填空题
|
函数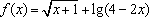
正确答案
解析
略
知识点
函数单调性的性质
1
题型：简答题
|
设a＞0，函数
（1）证明：存在唯一实数
（2）定义数列{xn}：x1=0，xn+1=f（xn），n∈N*。
（i）求证：对任意正整数n都有x2n﹣1＜x0＜x2n；
（ii） 当a=2时，若
正确答案
见解析。
解析
知识点
函数单调性的性质
1
题型：
单选题
|
已知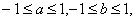
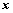
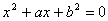
A
B
C
D
正确答案
A
解析
略
知识点
函数单调性的性质
1
题型：
单选题
|
如图，给定两个平面向量
A
B
C
D
正确答案
B
解析
略
知识点
函数单调性的性质
下一知识点 : 复合函数的单调性
扫码查看完整答案与解析