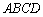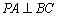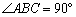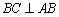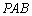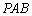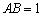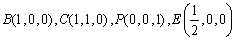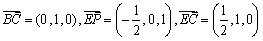- 函数单调性的性质
- 共479题
1
题型:简答题
|
已知数列


(1)求




(2)设



正确答案
见解析。
解析
(1)经计算



当



当



因此,数列

(2)


①、②两式相减,
得


知识点
函数单调性的性质
1
题型:
单选题
|
奇函数f(x)满足对任意x∈R都有f(2+x)+f(2-x)=0.且f(l)=2012,则f(2010)+f(2011)+
f(2012)的值为( )
正确答案
B
解析
略
知识点
函数单调性的性质
1
题型:
单选题
|
定义集合{x|a≤x≤b}的“长度”是b-a. 已知m,n∈R,集合

正确答案
C
解析
略
知识点
函数单调性的性质
1
题型:简答题
|
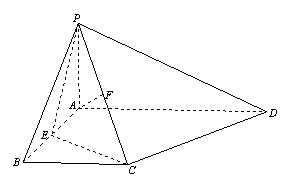
如图,在四棱锥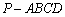
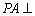
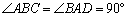
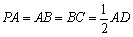
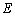
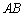
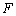
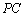
(1)求证: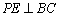
(2)求二面角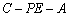
(3)若四棱锥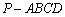
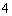
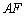
正确答案
见解析
解析
(1)∵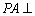
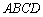
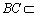
∴
∵
∴
∴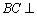
又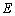
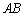
∴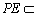
∴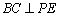
(2)建立直角坐标系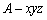
则
∴
由(1)知,
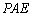
∴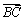
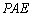
设平面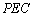
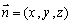
则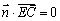
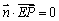
∴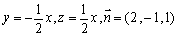
∴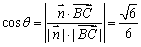
二面角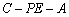
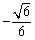
(3)连结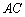
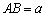
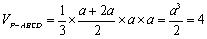
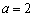
∵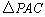
∴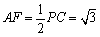
知识点
函数单调性的性质
1
题型:填空题
|
点P是抛物线y2=4x上一动点,则点P到点A(0,-1)的距离
与P到直线x=-l的距离和的最小值为 。
正确答案
解析
略
知识点
函数单调性的性质
下一知识点 : 复合函数的单调性
扫码查看完整答案与解析