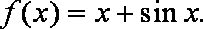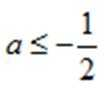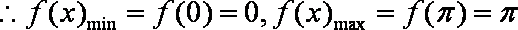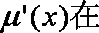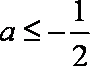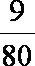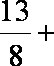- 函数单调性的性质
- 共479题
已知函数
(1)当
(2)设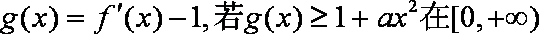
正确答案
(1)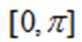
解析
(1) 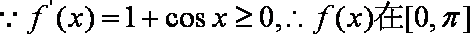
所以函数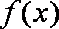
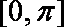
(2)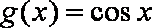
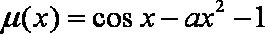
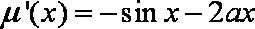
当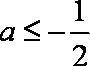
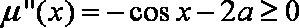
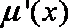
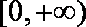
又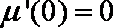
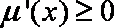
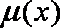
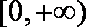
所以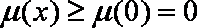
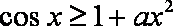
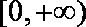
当
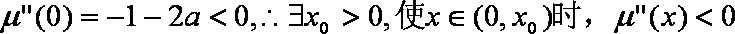
所以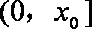
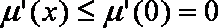
故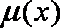
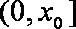
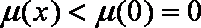
综上,故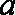
知识点
在平面直角坐标系









正确答案
见解析。
解析



即

直线

所以直线

知识点
设函数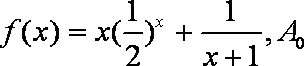
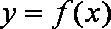
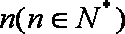
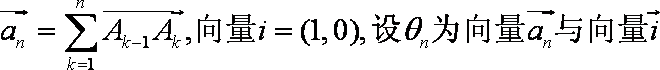

正确答案
解析
由题意知An=(n,f(n)),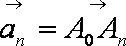
tanθn=
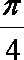
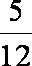
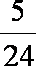
则有 1+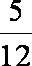
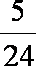
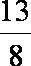

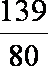
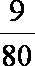
知识点
(1)求证:数列{an,-1)是等比数列;
(2)当n取何值时,bn取最大值,并求出最大值;
(3)若
正确答案
见解析
解析
(1)∵


∴

又



∵
∴


(2)由(1)可知


∴

当n=7时,

当n<7时,

当n>7时,

∴当n=7或n=8时,

(3)由

依题意(*)式对任意
①当t=0时,(*)式显然不成立,因此t=0不合题意,…………9分
②当t<0时,由


而当m是偶数时
③当t>0时,由

∴


设

∵

∴
∴

所以实数

知识点
已知点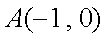
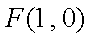
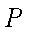
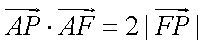
(1)求动点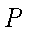
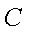
(2)在直线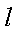
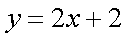
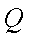
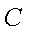
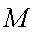
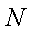
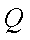
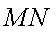
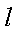
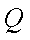
正确答案
见解析。
解析
(1)设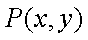
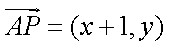
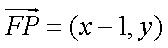
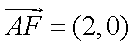
由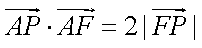
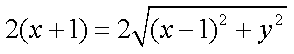
化简得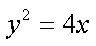
故动点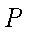
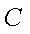
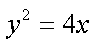
(2)直线
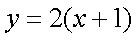
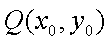
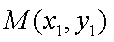
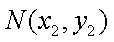
过点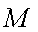
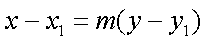
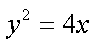
得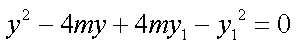
由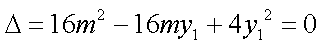
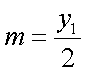
所以过点
同理过点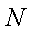
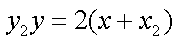
所以直线MN的方程为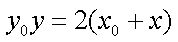
又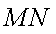
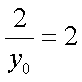
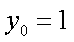
而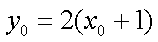
故点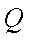
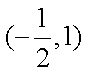
知识点
已知函数
(1) 试判断函数

(2) 若

(3) 求证:
正确答案
见解析
解析
解析:(1)


(2)


又

当
∴
(3)由(2)知
令
∴ln(1+1×2)+ln(1+2×3)+…+ln[1+n(n+1)]
∴(1+1×2)(1+2×3)…[1+n(n+1)]>e2n-3
知识点
若椭圆C:

(1) 求椭圆C的方程;
(2) 设点M(2,0), 点Q是椭圆上一点, 当|MQ|最小时, 试求点Q的坐标;
(3) 设P(m,0)为椭圆C长轴(含端点)上的一个动点, 过P点斜率为k的直线l交椭圆与A,B两点, 若|PA|2+|PB|2的值仅依赖于k而与m无关, 求k的值.
正确答案
解析
解析:(1)∵依题意a=5,c=3∴椭圆C的方程为: 
(2)设Q(x,y), -5≤x≤5
∴|MQ|2=(x-2)2+y2=x2-4x+4+16-x2=x2-4x+20
∵对称轴x=>5∴当x=5时, |MQ|2达到最小值,
∴当|MQ|最小时, Q的坐标为(5,0) ························6
知识点
已知







(1)求椭圆C的方程;
(2)若记


正确答案
见解析
解析
(1)令


(2)
由方程组


①2/②得


知识点
已知平面向量









正确答案
解析
如图,设







知识点
设



(1)求函数
(2)证明:对任意正数


(3)设



正确答案
见解析
解析
(1)∵
由

∴


故当



∴当


(2)∵
又当



因此原不等式化为
即
令

由


当



故当


令

故

因此,存在正数
(3)由(1)

取

即
法二:先证
令

则





∴

则有
知识点
扫码查看完整答案与解析