- 空间点、线、面的位置
- 共6题
如图,四棱锥P-ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=
(1)求PA的长;
(2)求二面角B-AF-D的正弦值。
正确答案
(1) 
解析
(1)
如图,连接BD交AC于O,因为BC=CD,即△BCD为等腰三角形,又AC平分∠BCD,故AC⊥BD。以O为坐标原点,







因PA⊥底面ABCD,可设P(0,-3,z),由F为PC边中点,F
又



因AF⊥PB,故

即6-


所以|

(2)由(1)知





由n1·

因此可取n1=(3,
由n2·

得

从而法向量n1,n2的夹角的余弦值为
cos〈n1,n2〉=
故二面角B-AF-D的正弦值为
知识点
如图,在直三棱柱









(1)求异面直线

(2)求点

正确答案
(1)
解析
(1)设







连接ME,在
所以异面直线


(2)

以点






设平面
则
所以平面

又
所以点


知识点
如图,在直三棱柱ABC﹣A1B1C1中,AB=4,AC=BC=3,D为AB的中点
(1)求点C到平面A1ABB1的距离;
(2)若AB1⊥A1C,求二面角A1﹣CD﹣C1的平面角的余弦值。
正确答案
见解析
解析
(1)由AC=BC,D为AB的中点,得CD⊥AB,又CD⊥AA1。
故CD⊥平面A1ABB1。
所以点C到平面A1ABB1的距离为CD=
(2)解法一:如图1,取D1为A1B1的中点,连接DD1,则DD1∥AA1∥CC1。
又由(1)知CD⊥平面A1ABB1,故CD⊥A1D,CD⊥D1D,所以∠A1DD1为所求的二面角A1﹣CD﹣C1的平面角,因A1D为A1C在面A1ABB1中的射影,又已知AB1⊥A1C由三垂线定理的逆定理得AB1⊥A1D,从而∠A1AB1、∠A1DA都与∠B1AB互余,因此∠A1AB1=∠A1DA,所以Rt△A1AD∽Rt△B1A1A,因此AA1:AD=A1B1:AA1,即AA12=AD•A1B1=8,得AA1=2




解法二:如图2,过D作DD1∥AA1交A1B1于D1,在直三棱柱中,有DB,DC,DD1两两垂直,以D为原点,射线DB,DC,DD1分别为X轴、Y轴、Z轴的正半轴建立空间直角坐标系D﹣xyz。
设直三棱柱的高为h,则A(﹣2,0,0),A1(﹣2,0,h),B1(2,0,h),C(0,




由AB1⊥A1C,可得8﹣h2=0,h=2





设平面A1CD的法向量为



∴ 






设平面C1CD的法向量为







所以cos<




知识点
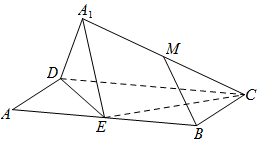
如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE。
(1)当平面A1DE⊥平面BCD时,求直线CD与平面CEA1所成角的正弦值;
(2)设M为线段A1C的中点,求证:在△ADE翻转过程中,BM的长度为定值。
正确答案
见解析。
解析
解:
(1)过A1作A1F⊥DE,由已知可得A1F⊥平面BCD,且F为DE中点,以D为原点,DC、DA所在直线为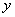

求得平面CEA1的一个法向量为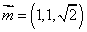
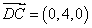
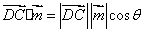
所以,直线CD与平面CEA1所成角的正弦值为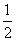
(2)取A1D中点G,连结MG,EG,由MG∥EB,且MG=EB,可得BMGE为平行四边形,所以,BM=EG,而三角形ADE中,EG的长度为定值,所以,BM的长度为定值。
知识点
16.用一个边长为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析