热门试卷

1 填空题 · 4 分

16．在平行六面体的一个面所在的平面内，任意画一条直线，则与它异面的平行六面体的棱的条数可能是____________（填上所有可能结果）。

1 单选题 · 5 分

9.从正方体的棱和各个面的面对角线中选出条，使得其中任意两条线段所在的直线都是异面直线，则的最大值是（）

1 填空题 · 4 分

5．在的取值范围为_______

1 简答题 · 12 分

某象棋比赛规则如下：两名选手比赛时，每局胜者得1分，负者得分，比赛进行到有一人比对方多分或打满局时结束.假设选手甲与选手乙比赛时，甲、乙每局获胜的概率分别为和，且各局比赛胜负互不影响.

（1）求比赛进行局结束，且乙比甲多得分的概率；

（2）设表示比赛停止时已比赛的局数，求随机变量的分布列和数学期望。

1 简答题 · 12 分

已知公比不为的等比数列的首项，前项和为，且成等差数列。

（1）求等比数列的通项公式；

（2）对，在与之间插入个数，使这个数成等差数列，记插入的这个数的和为，求数列的前项和。

1 简答题 · 14 分

如图，在直三棱柱中，，，，点分别在棱上，且。

（1）求四棱锥的体积；

（2）求所在半平面与所在半平面所成二面角的余弦值。

1 简答题 · 12 分

如图，已知正方形ABCD的边长为6，点E,F分别在边AB,AD上，，现将沿线段EF折起到位置，使得.

（1）求五棱锥的体积;

（2）求平面与平面的夹角.

1 简答题 · 10 分

如图，平面平面ABC，是等腰直角三角形，AC =BC= 4，四边形ABDE是直角梯形，BD∥AE，BD BA，,，

求直线CD和平面ODM所成角的正弦值。

1 简答题 · 12 分

如图，在斜三棱柱中，点、分别是、的中点，平面.已知，.

（1）证明：平面；

（2）求异面直线与所成的角；

（3）求与平面所成角的正弦值。

1 填空题 · 3 分

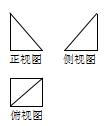
12．一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，若要拼成一个棱长为1的正方体，则需要这样的几何体（）个。

继续学习学习下一知识点

下一知识点 : 空间中直线与直线之间的位置关系

百度题库 > 高考 > 理科数学 > 异面直线的判定

扫码查看完整答案与解析