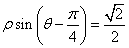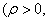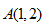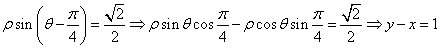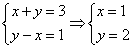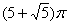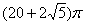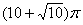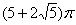- 组合几何体的面积、体积问题
- 共83题
如图,底面是等腰梯形的四棱锥E—ABCD中,EA


(1)设F为EA的中点,证明:DF//平面EBC;
(2)若AE=AB=2,求三棱锥—CDE的体积。
正确答案
见解析。
解析
知识点
一个长方体被一平面截去一部分所得几何体的三视图如右图,
则该几何体的体积是:
正确答案
解析
略
知识点
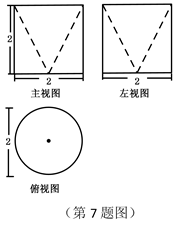
若一个空间几何体的三视图如图所示,则这个几何体的表面积为()
正确答案
解析
略
知识点
若用一个平面去截球体,所得截面圆的面积为

正确答案
100p
解析
略
知识点
若以直角坐标系的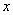
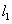
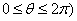
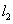
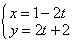
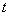
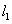
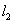
正确答案
解析
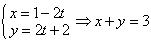
知识点
一个几何体的三视图如图1,则该几何体
的体积为
正确答案
解析
略
知识点
如图










(1)求证:

(2)求证:

(3)求五面体
正确答案
见解析。
解析
(1)证明:连接






∵

∴


∵





∴

∵
∴


∴四边形
∴


∵



∴

(2)证法1:取



由(1)知,


∴四边形
∴


在Rt△



∴
在△



∴
∴
∴

∵四边形
∴
∵




∴

证法2:在Rt△


∴
在△

∴
∴
∵

∴
∵




∴

∵

∴
∵四边形
∴
∵




∴

(3)
解:连接
在Rt△

∴
由(2)知



∴

∵



∴

∴四棱锥

∴三棱锥

∴五面体

知识点
如图,正方形ADEF所在平面和等腰梯形所在平面ABCD垂直,已知BC=2AD=4,
(1)
(2)求异面直线BE与AF所成的角;
(3)求该几何体的表面积。
正确答案
见解析。
解析
知识点
某几何体的三视图如右图所示,则该几何体的表面积为
正确答案
解析
略
知识点
最近科学家获得了一种稳定性好、抗氧化能力强的活性化合物,其结构如下:
在研究其性能的过程中,发现结构片段X对化合物A的性能有重要作用。为了研究X的结构,将化合物A在一定条件下水解只得到B和C。经元素分析及相对分子质量测定,确定C的分子式为C7H6O3,C遇FeCl3水溶液显紫色,与NaHCO3溶液反应有CO2产生。
请回答下列问题:
(1)化合物B能发生下列哪些类型的反应 。
a取代反应 b.加成反应 c 缩聚反应 d氧化反应
(2)写出化合物C所有可能的结构简式 。
(3)化合物C能经下列反应得到G(分子式为C8H6O2,分子内含有五元环);
①确认化合物C的结构简式为 。
②F
③化合物E有多种同分异构体,
正确答案
(1)a b d
(2)C所有可能的结构简式为:
(3)
解析
题给信息:
1、A→B+C,根据A与B的结构的区别,此反应为酯的水解反应,A含羟基则C含羧基。
2、C的分子式为C7H6O3,缺氢分析(16-6)/2=5,结构中含有苯环和羧基。
3、C遇FeCl3水溶液显紫色,与NaHCO3溶液反应有CO2产生。
根据2、3可以判断C的结构中韩苯环、酚羟基、羧基。
(1)化合物B含碳碳双键和醇羟基,而且是伯醇羟基。所以只有缩聚反应不能发生。
知识点
扫码查看完整答案与解析