裂项相消法求和
共32题

· 裂项相消法求和

裂项相消法求和
共32题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

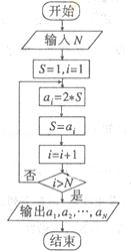
根据如图框图，对大于2的正数N，输出的数列的通项公式是（　　）

Aan=2n

Ban=2（n﹣1）

Can=2n

Dan=2n﹣1

正确答案

解析

由程序框图知：ai+1=2ai，a1=2，

∴数列为公比为2的等边数列，∴an=2n。

知识点

裂项相消法求和

题型：简答题

简答题 · 12 分

设F1，F2分别是C：+=1（a＞b＞0）的左，右焦点，M是C上一点且MF2与x轴垂直，直线MF1与C的另一个交点为N。

（1）若直线MN的斜率为，求C的离心率；

（2）若直线MN在y轴上的截距为2，且|MN|=5|F1N|，求a，b。

正确答案

（1）e=

（2）a=7，b=

解析

（1）∵M是C上一点且MF2与x轴垂直，∴M的横坐标为c，当x=c时，y=，即M（c，），

若直线MN的斜率为，即tan∠MF1F2=，即b2==a2﹣c2，即c2﹣﹣a2=0，

则，解得e=。

（2）由题意，原点O是F1F2的中点，则直线MF1与y轴的交点D（0，2）是线段MF1的中点，故=4，即b2=4a，

由|MN|=5|F1N|，解得|DF1|=2|F1N|，设N（x1，y1），由题意知y1＜0，

则，即代入椭圆方程得，

将b2=4a代入得，解得a=7，b=

知识点

裂项相消法求和

题型：简答题

简答题 · 12 分

已知等差数列满足：，.的前n项和为.

（1）求及；

（2）令（）,求数列的前n项和.

正确答案

见解析。

解析

（1）设等差数列的公差为d，因为，，所以有

，解得，

所以；==。

（2）由（1）知，所以bn===，

所以==，

即数列的前n项和=。

知识点

由数列的前几项求通项等差数列的性质及应用等差数列的前n项和及其最值裂项相消法求和

题型：简答题

简答题 · 14 分

已知数列满足

（1）求的值；

（2）设，证明是等比数列；

（3）设为的前项和，证明

正确答案

见解析

解析

（1）解：由，可得

又，

当

（2）证明：对任意

①

②

②-①，得

所以是等比数列。

（3）证明：，由（Ⅱ）知，当时，

故对任意

由①得

因此，

于是，

故

知识点

裂项相消法求和

题型：简答题

简答题 · 14 分

已知正项数列中，，前n项和为，当时，有.

（1）求数列的通项公式；

（2）记是数列的前项和，若的等比中项，求。

正确答案

见解析。

解析

（1）

，

（2）

知识点

由递推关系式求数列的通项公式裂项相消法求和

继续学习学习下一知识点

下一知识点 : 倒序相加法求和

百度题库 > 高考 > 文科数学 > 裂项相消法求和

扫码查看完整答案与解析