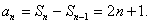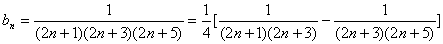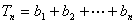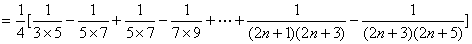- 裂项相消法求和
- 共32题
1
题型:简答题
|
在数列




(1)求
(2)设


正确答案
见解析。
解析
(1)∵

∴
又



当


(2)由(1)知,
∴
∴
知识点
裂项相消法求和等差数列与等比数列的综合
1
题型:简答题
|
已知数列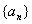
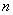
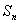
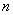
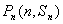
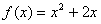
(1)求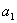
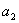
(2)求数列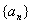
(3)若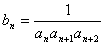
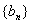
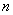
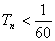
正确答案
见解析。
解析
(1)∵点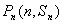
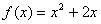
∴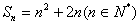
∴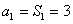
又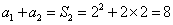
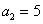
(2)由(1)知,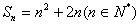
当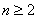
由(1)知,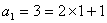
所以数列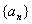
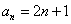
(3)由(2)得
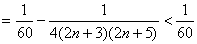
知识点
由an与Sn的关系求通项an裂项相消法求和数列与不等式的综合
1
题型:简答题
|
已知数列





(1)求

(2)记数列




正确答案
见解析。
解析
(1)因为



又
得

(2)因为
而

知识点
由递推关系式求数列的通项公式裂项相消法求和数列与不等式的综合
1
题型:简答题
|
已知数列






(1)求
(2)求证:数列
(3)求使

正确答案
见解析
解析
(1) 由


故
(2)由
得 

即

,故
(3) 由(2)得

故 


知识点
裂项相消法求和
1
题型:简答题
|
已知数列
(1)求数列
(2)若


正确答案
见解析。
解析
(1)


(1)-(2)得
又
(2)
知识点
由递推关系式求数列的通项公式裂项相消法求和
下一知识点 : 倒序相加法求和
扫码查看完整答案与解析